Study on numerical simulation of rock breaking by PDC wear teeth cutting
-
摘要: 现有文献针对切削齿的数值模拟研究较少考虑磨损高度对切削齿温度、切削载荷的影响，然而聚晶金刚石复合片（PDC）切削齿磨损后受力恶化、热磨损加剧会导致其快速失效。为探讨这一问题，基于弹塑性力学和岩石力学，以Drucker-Prager准则为岩石的本构模型建立磨损齿的三维动态旋切仿真模型，运用数值模拟的方法分析在不同磨损高度、切削深度、前倾角的条件下切削齿的受力状态以及温升幅度。结果表明：与未磨损齿相比，磨损齿的切削载荷随磨损高度的增加而变大，且切削齿（直径13.4 mm、总高8 mm）磨损高度为1.5 mm时达到最大；切削齿磨损越严重，吃入到同一深度所需的力越大；前倾角增加，导致切削载荷也会变大。因此磨损齿在切削钻进过程中，磨损高度越高、前倾角越大，切削齿的失效风险越高；随着切削齿磨损高度增加，切削齿温升显著增加，在模拟条件下可提高54%～103%。
-
关键词:
- PDC切削齿 /
- Drucker-Prager准则 /
- 单齿切削 /
- 切削载荷 /
- 切削热
Abstract: Objectives: The existing literature on numerical simulation of cutters rarely considers the effect of wear height on the temperature and cutting load of cutters. However, the deterioration of force and the aggravation of thermal wear after the wear of polycrystalline diamond composite (PDC) cutters lead to their rapid failure. Therefore, it is particularly necessary to study the change of cutting load and the law of heat generation of worn cutters to extend their service life. Methods: Based on elastoplastic mechanics and rock mechanics, a 3D dynamic rotational simulation model of worn teeth is established with the Drucker-Prager criterion as the rock constitutive model. The stress state and temperature rise amplitude of cutting teeth under different wear heights, cutting depths, and front inclination angles are analyzed by numerical simulation. Results: (1) Influence of wear height on cutting load: Under simulated conditions (front inclination 15°, cutting depth 1.5 mm), the size and the fluctuation degree of cutting load increase with the increase of wear height when the wear height is 0−1.5 mm, and decrease slightly when the wear height is larger than 1.5 mm. In terms of tangential force, the cutter with a wear height of 1.5 mm is subjected to the largest tangential force, but when the wear height is 2.0 mm, the tangential force is reduced. In terms of axial force, the axial force of worn teeth is higher than that of unworn teeth. When the wear height is 0−1.5 mm, the axial force gradually increases with the increase of wear height. When the wear height is 1.5 mm, the axial force reaches its maximum, and when the wear height is larger than 1.5 mm, the axial force decreases. The axial force of the cutter with a wear height of 1.0 mm and wear height of 2.0 mm is exactly 1.2 times that of the unworn tooth, and the axial force of the cutter with a wear height of 1.5 mm is 1.3 times that of the unworn tooth. (2) Influence of cutting depth on cutting load: Under simulated conditions (wear height 1.0 mm, front inclination angle 15°), tangential force and axial force gradually increase with the increase of cutting depth, and the degree of fluctuation is more intense. In terms of tangential force, the tangential force of the worn tooth with the cutting depth of 2.0 mm is 1.9 times that of the worn tooth with the cutting depth of 1.0 mm, and the increase is larger. The tangential force of the worn tooth with the cutting depth of 1.5 mm is only 25% higher than that of the worn tooth with the cutting depth of 1.0 mm, and the increase is small. In terms of axial force, with the increase of cutting depth, the increase in axial force is relatively balanced. (3) Influence of front inclination angle on cutting load: Under simulated conditions (wear height 1.0 mm, cutting depth 1.5 mm), the cutting load of worn teeth gradually increases with the increase of front inclination angle, with the tangential force increasing by 28% and the axial force increasing by 32%. When the front angle is 10°, the fluctuation of the cutting load is more severe than at other time with 15° and 20°. (4) Influence of wear height on cutting heat: according to the temperature cloud map of the cutter, because the cutter rotates around the central axis to break rock, the linear speed of the cutting edge differs, and the temperature on the side away from the central axis will be higher than that on the side near the central axis. With the increase of wear degree, the temperature rise of the cutter becomes more significant, and the high-temperature area is concentrated in the cutting-cutter contact area, where plastic deformation and frictional heat generation are concentrated. The temperature change curve can be divided into three stages: rising period, transitional period, and stable period. With the passage of time, the temperature of the cutter continues to rise, and the temperature rise rate in the rising period is greater than in the transitional period, tending to flatten after entering the stable period. In the process of rock breaking, the temperature rise of worn teeth is much higher than that of unworn teeth, with a temperature increase of 54%−103%. Conclusions: The force on a cutter with excessive wear is more complex and variable, increasing the risk of fatigue failure. In terms of tooth layout, it can be considered to place the auxiliary cutting unit behind the main cutting unit composite sheet and make its exposure height lower than the composite sheet, which can effectively reduce the load on the main cutting gear and reduce the probability of overload damage to the cutting gear. The cutting load of the worn teeth increases with the increase of the front angle. Considering the fluctuation of cutting efficiency and load, the front angle should be controlled at 15°−20° as far as possible, which is beneficial to prolong the service life of the cutting teeth. After cutter wear, its ability to break rock is weakened, the rock pre-crushing area is reduced, and the way of cutting the rock gradually transitions from shear failure to extrusion failure, greatly reducing the rock-breaking efficiency of the cutter. In the process of cutting rock breaking, the temperature rise of the worn teeth is much higher than that of the unworn teeth, and the temperature rise increases with the increase of wear degree. Thus, the thermal wear of the cutting teeth will continue to intensify after wear, accelerating the wear and failure of the cutting teeth. In the subsequent cutting process, cutter of wear-resistant and high-temperature-resistant materials can be selected to reduce the weight on the bit and the speed of drilling while increasing the water power of the pump, effectively inhibiting thermal wear.-
Key words:
- PDC cutter /
- Drucker-Prager criterion /
- single tooth cutting /
- cutting load /
- cutting heat
-
目前，聚晶金刚石复合片（polycrystalline diamond compact，PDC）钻头凭借其钻速快、使用寿命长的优势特性在油气钻井、煤田钻探、地质勘探中得到广泛应用，其在油气钻井领域以80%以上的国际市场占有率和90%以上的进尺引领了全球钻头市场[1]。同时，深地层岩石非均质性强、研磨性强等特点也限制了PDC钻头的钻进效率[2]，切削齿的快速磨损是其中的一个关键原因。70%以上的PDC钻头损坏是PDC钻头切削齿失效造成的，主要表现为切削齿的磨损和断裂[3]。切削齿作为PDC钻头的基本组成部分，研究磨损切削齿的切削载荷变化和生热规律显得尤为必要。
在单齿切削钻进方面，国内外研究者进行了较为细致的探讨。邓敏凯等[4]通过仿真模拟与实验结合，研究了侧倾角和前倾角的变化对PDC钻头切削齿破岩效果的影响规律，结果表明，前倾角为15°～20°、侧倾角为5°时，切削齿的破岩效果最好且切削齿寿命较长。祝效华等[5]通过数值模拟探究切削深度、后倾角、侧倾角等因素对破岩能效的影响，结果表明，随着后倾角的增大，破碎比功逐渐增大且基本不受切削深度和围压的影响；切削齿存在最优切削深度2 mm，其破碎比功最小。杨迎新等[6]用不同磨损程度的切削齿进行单齿切削实验，结果表明，与未磨损齿相比，磨损齿所受切削力更大，切削力波动和温度变化也更明显，且易发生体积破碎，产生大体积岩屑。赵润琦等[7]通过数值模拟的研究方法，发现斧形PDC齿在破碎同等体积的岩石时比常规平面PDC齿所需的切削力更低，且更易钻入岩石。张春亮等[8]通过单齿切削实验和全尺寸磨损齿钻头钻进实验研究了磨损齿PDC钻头的切削性能，结果表明，随着磨损程度的增加，切削齿的载荷波动明显，钻头的机械钻速下降，机械比能增加，振动程度减少。ROSTAMSOWLAT等[9]使用未磨损切削齿与磨损切削齿分别对石灰岩和砂岩进行单齿切削，研究了不同切削深度下磨损齿的磨损表面与岩石表面形成的夹角对切削过程中摩擦力大小的影响。
在破岩产生切削热方面，朱光辉等[10]用不同前倾角、不同磨损程度的切削齿进行了切削试验和温度监测，结果表明，切削齿的磨损程度越严重、前倾角越大，相较于未磨损齿的切削力和温度变化越大。VORONTSOV等[11]探究了单齿破岩时切削齿温度随前倾角变化的规律。邓嵘等[12]运用有限元仿真分析方法，研究了单齿动态破岩中切削齿的温度分布情况，结果表明，因线速度不同，切削区域远离钻头轴线一侧的温升高于靠近轴线一侧的。MAMALIS等[13]运用有限元仿真方法，研究了高速切削情况下切削齿的破岩功与切削热量的转化关系。张在兴等[14]通过仿真方法研究了切削角度对切削齿温度波动程度的影响规律，结果表明，当切削角度大于临界值时，切削齿的温度会随着切削角度的增大而降低。
现有研究大多是对切削齿的单齿破岩数值模拟研究或磨损切削齿的单齿破岩实验研究，鲜有研究者将切削齿磨损状态与切削热同时考虑入破岩数值模拟研究中。PDC切削齿磨损状态下的破岩数值模拟得出的切削载荷和温度变化情况与磨损程度的关系尚不明确，亟待开展深入研究。因此，本研究中使用切削齿进行单齿破岩模拟，并重点分析不同的磨损高度、前倾角、切削深度等因素对PDC磨损齿切削载荷和温度变化的影响规律。
1. 有限元破岩模型
1.1 模型假设
模型的参数设置如表1所示，为了便于计算和分析，对有限元破岩过程做以下假设：（1）岩石属性设置为连续的、各向同性的介质，且为均质弹塑性体；（2）忽略实际切削岩石的孔隙压力效应，且不含层理、裂缝或溶洞等特殊结构；（3）岩石单元失效后立即从岩体中删除，不计其失效后对切削的影响；（4）将切削齿视为刚体，钻进过程中不发生损耗。
表 1 PDC切削齿和岩石的参数Table 1. Parameters of PDC cutters and rocks材 料 PDC 岩石 密度ρ / (kg·m−3) 3 510 2 580 弹性模量 E / GPa 890 25 泊松比 ν 0.077 0.150 热传导率 λ /（W·m−1·℃−1） 543.0 3.5 比热容 c /(J·kg−1·℃−1) 790 800 热膨胀系数 α / ℃−1 2.5 × 10−6 12.0 × 10−6 内摩擦角 φ / (°) — 42 抗压强度 σ bc/ MPa — 40 1.2 岩石与切削齿物理模型
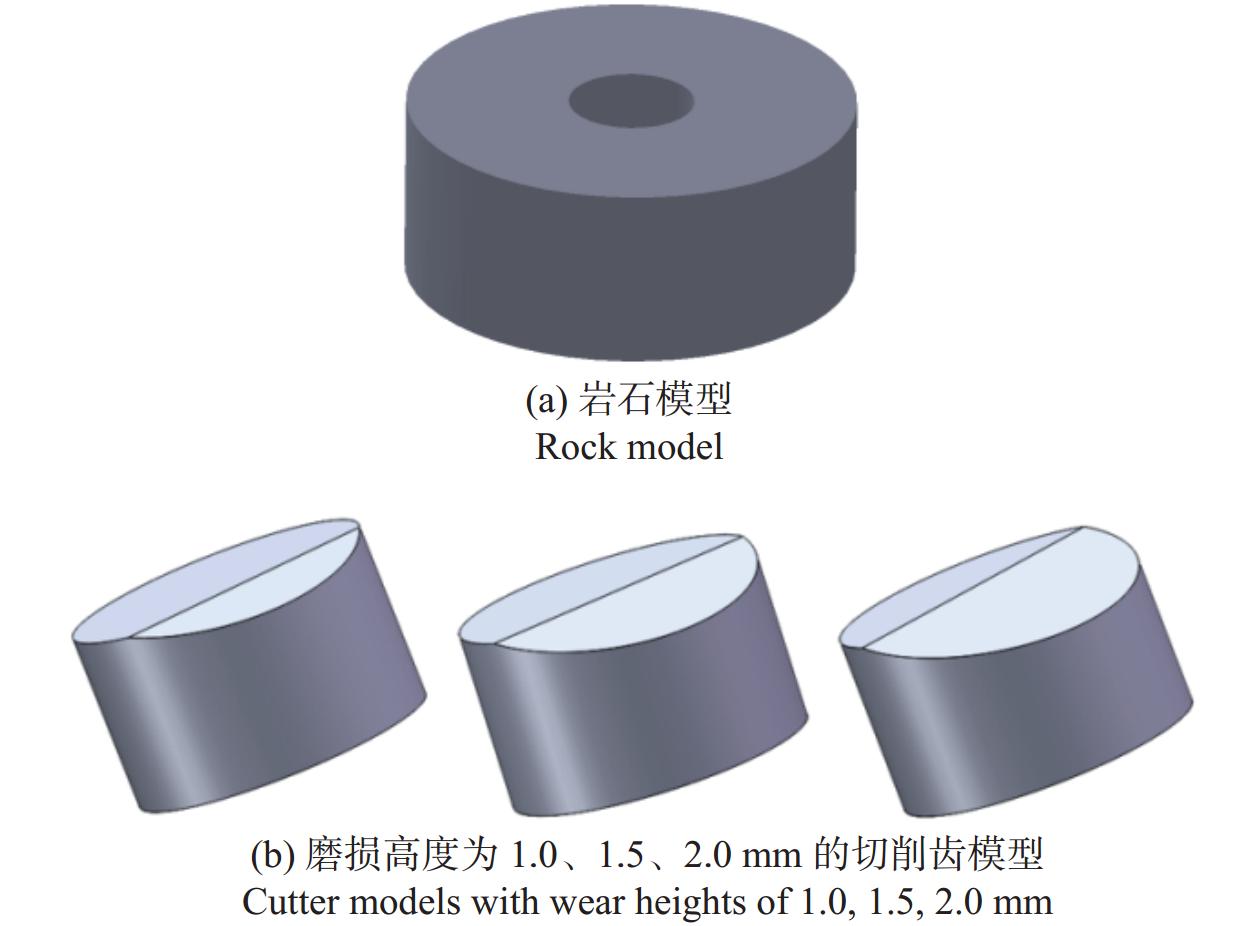
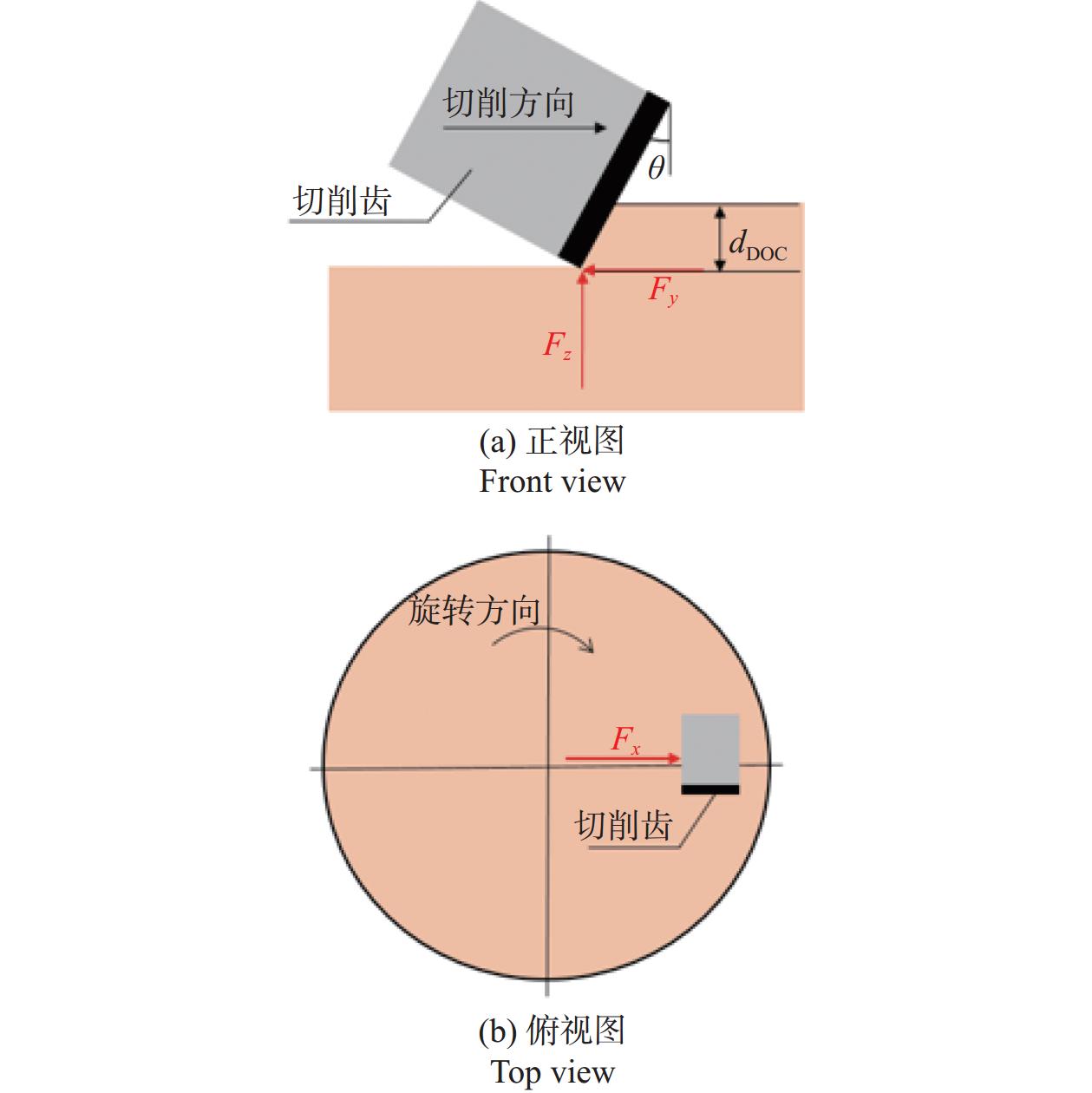
根据圣维南原理，为了减少局部效应对破岩真实性的影响，岩石的模型尺寸应比切削齿大4～7倍[7]。考虑到计算机的求解速度，模拟的岩石选取外直径为100 mm、内直径为28 mm、高度为40 mm的几何体。切削齿选取直径为13.4 mm、高度为8 mm的磨损平面切削齿。岩石与切削齿的物理模型如图1所示。
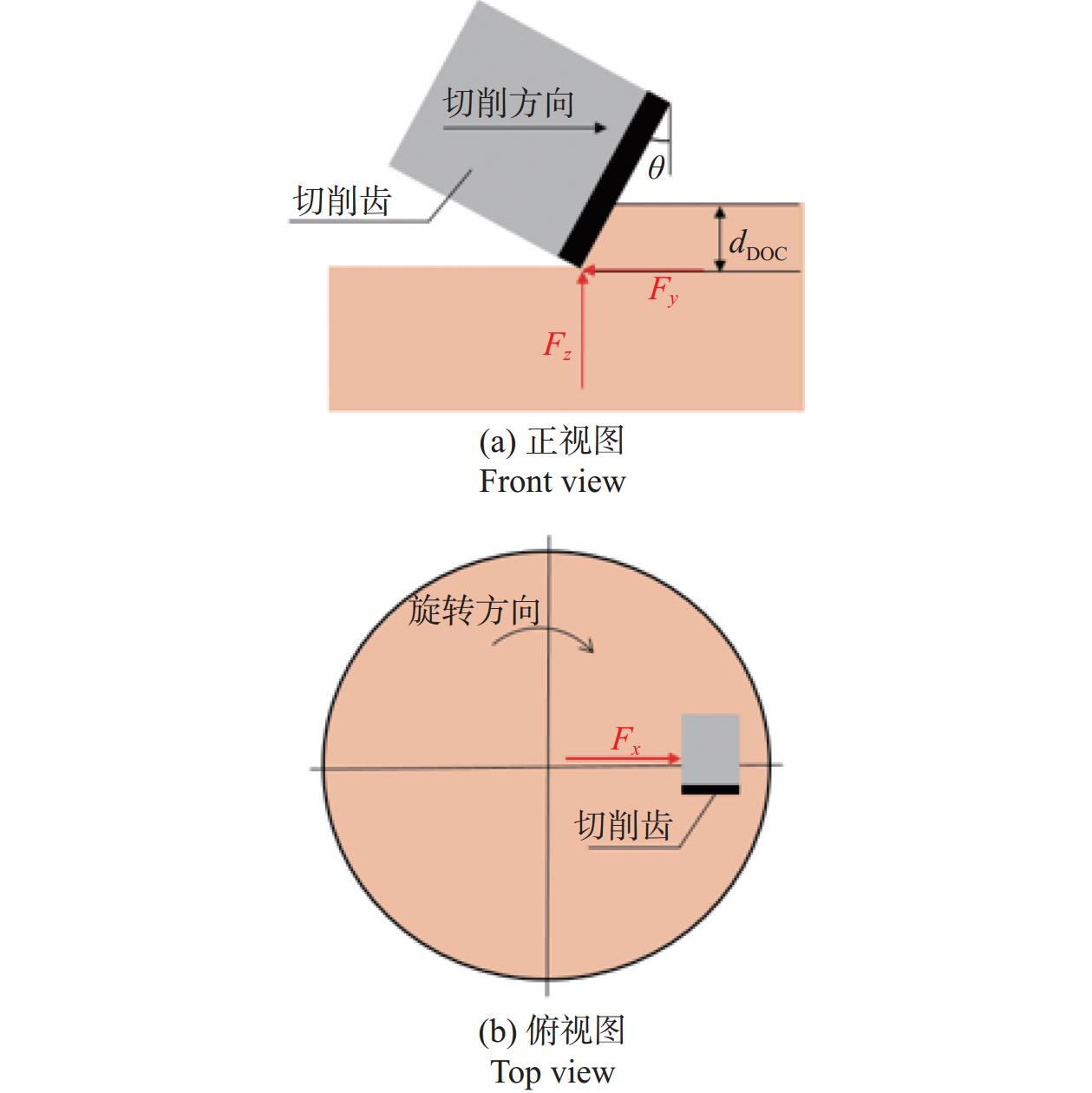
建立的切削齿与岩石的破岩受力分析如图2所示，dDOC为切削深度，θ为前倾角。切削齿在破岩过程中，受到侧向力Fx、切向力Fy与轴向力Fz的共同作用。Fx垂直于旋切轨迹并指向外侧，Fy与旋转方向相反，Fz垂直于Fy并指向切削齿。
1.3 岩石强度准则及相互作用模型
岩石模型采用Drucker-Prager弹塑性和剪切损伤相结合的本构模型，并定义了硬化特征。D-P模型考虑了中间应力的作用以及岩石剪胀现象，并且可以将试验获得的M-C准则数据与D-P准则进行相互转换[15]，D-P准则表达式[7]为：
$$ F=t-p\text{tan}\ \beta-d=0 $$ (1) $$ G=t-p\text{tan }\varphi $$ (2) $$ t=\frac{q}{2}\left[1+\frac{1}{K}-\left(1-\frac{1}{K}\right) \frac{r^3}{q}\right] $$ (3) 式中：F为屈服面函数，t为偏应力参数，p为等效压应力，β为p-t应力平面中的岩石膨胀角，d为屈服面在p-t应力平面中t轴的截距，G为塑形势面函数，φ为p-t应力平面中的内摩擦角，q为等效米塞斯应力，K为流应力比，r为偏应力的第三不变量。
硬化函数[16]可以表示为：
$$ \kappa=\sigma_0+\kappa_c $$ (4) $$ \sigma_0=\frac{6 c \cos \varphi}{\sqrt{3}(3-\sin \varphi)} $$ (5) 式中：$ \kappa $为硬化函数，$ \sigma_0 $为Drucker-Prager屈服准则圆锥面与Mohr Coulomb屈服准则六角棱锥外接时的取值，$ {\kappa}_{{c}} $为岩石的摩擦硬化或软化塑性内变量，c为岩石内聚力。
仿真实验采用剪切损伤作为岩石失效条件，并设定损伤演化参数，即当岩石破坏位移等于失效位移时，岩石单元立即被移除。为得到更加精确的仿真结果，本模型采用C3D8RT八结点热耦合六面体单元网格对岩石模型进行网格划分，岩石与切削齿接触区域进行了0.3～0.8 mm小尺寸网格局部加密，以模拟破岩时岩屑的形成。
该切削齿破岩模型已给定机械钻速和转速，所以切削齿切削深度[17]可表示为：
$$ d_{\mathrm{DOC}}=\frac{v_{\mathrm{ROP}}}{N}=\frac{v_{\mathrm{ROP} }t}{N t}=\frac{h}{n} $$ (6) 式中：$ {{d}}_{\text{DOC}} $为切削深度，mm；vROP为机械钻速，mm·min−1；N为转速，r·min−1；t为时间，min；h为切削齿进尺，mm；n为转数。
设定切削齿绕岩石模型中心轴逆时针匀速旋转720°吃入岩石，并设置仿真时间为1 s，切削齿进尺为2、3、4 mm，由式（6）可得切削深度$ {d}_{\text{DOC}} $分别固定为1.0、1.5、2.0 mm。岩石的边界条件设置为完全固定，最终切削齿破岩数值模拟模型如图3所示。
图 3 PDC切削齿破岩数值模拟模型Figure 3. Numerical simulation model of rock breaking for PDC cutter1.4 数值模拟方案拟定
磨损切削齿在破岩过程中的切削载荷和温度受诸多因素的影响，选择性研究对其影响较大的因素，如磨损高度、前倾角、切削深度等。模拟过程中，为了顺利得到各因素对切削载荷以及温度变化的影响规律，将其设置为唯一变量，具体的破岩仿真方案如表2所示。
表 2 切削齿破岩仿真方案Table 2. Simulation scheme of cutter rock breaking仿真方案 仿真参数 磨损高度 H / mm 前倾角 θ / (°) 切削深度 dDOC / mm 方案一 0、1.0、1.5、2.0 15 1.5 方案二 1.0 10、15、20 1.5 方案三 1.0 15 1.0、1.5、2.0 2. 有限元模拟结果分析与讨论
围绕磨损高度、切削深度和前倾角对切削齿的切削载荷与温度变化的影响以及破岩能力进行评价。由以往文献[8]可知，切削载荷会随时间变化剧烈波动，这是因为在应力达到岩石的屈服极限后，岩石单元会断裂破坏并被删除，切削齿受到的切削载荷迅速下降，接着对下一部分的岩石单元进行切削，切削载荷又会振荡。因此对切削载荷进行了平滑处理 ，这样更利于得出切削载荷随自变量变化的规律。
2.1 岩石应力场特征
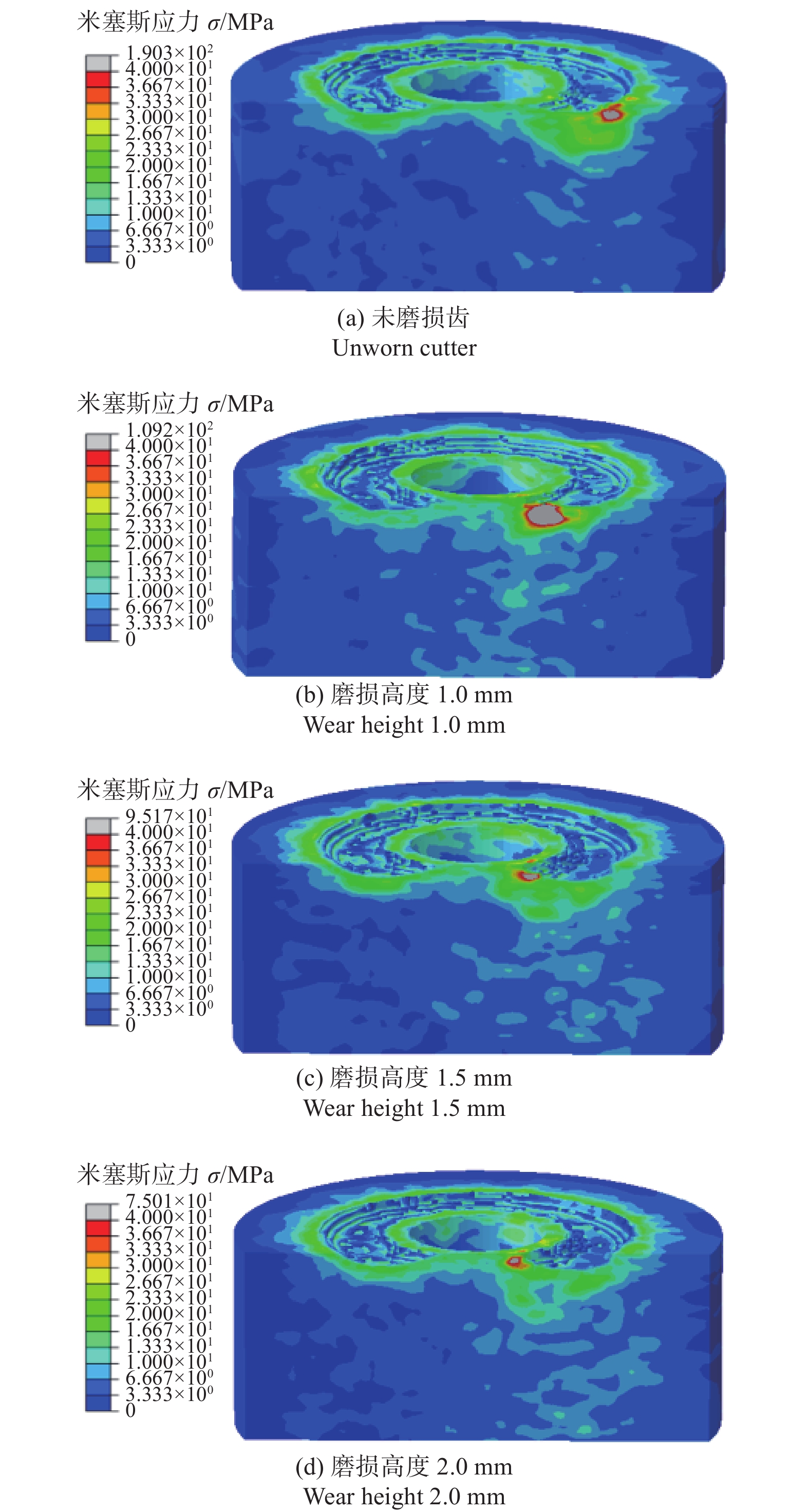
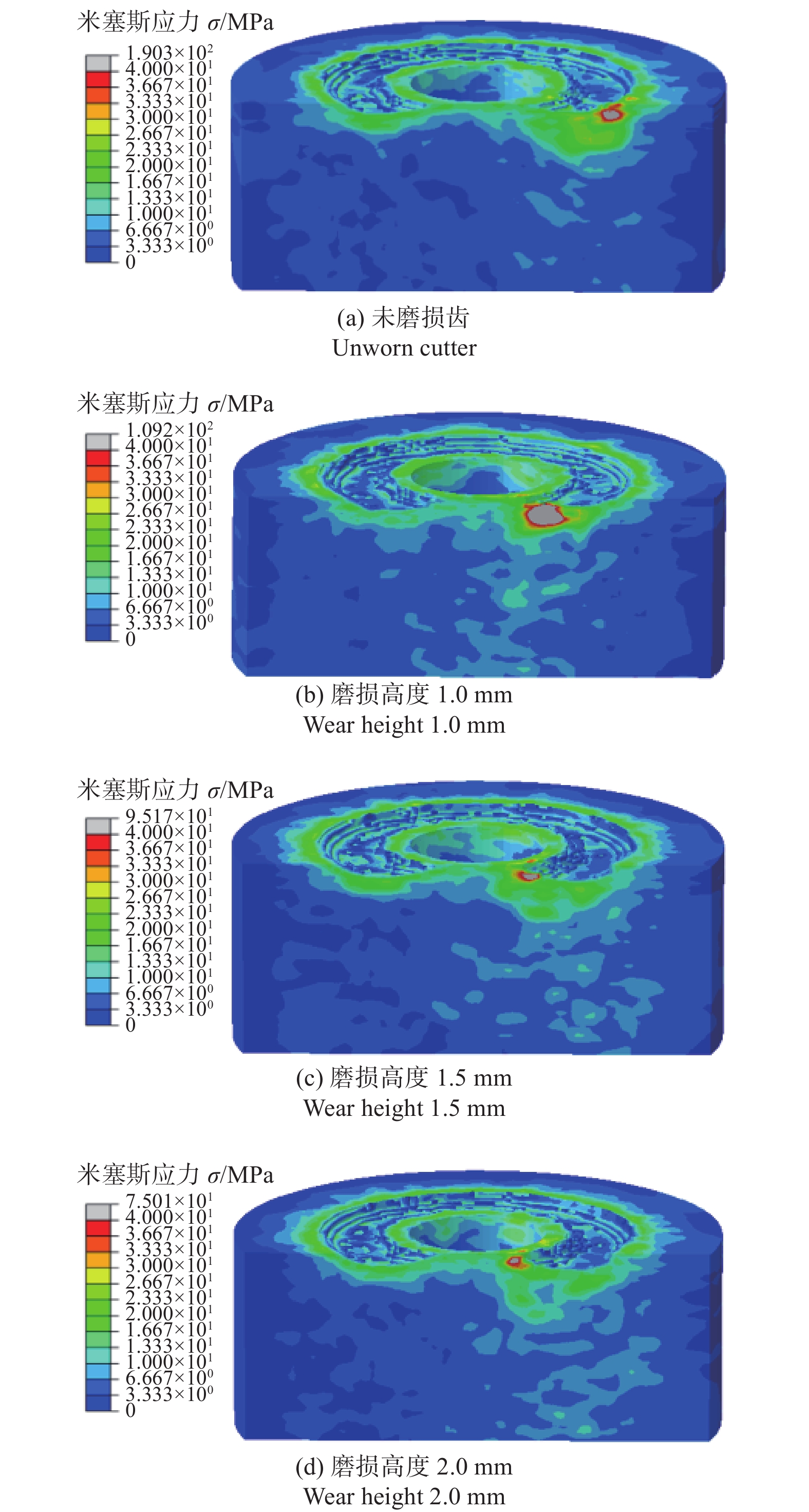
在模拟条件（前倾角15°、切削深度1.5 mm）下，切削齿吃入岩石时的应力场分布情况如图4所示。由图4可知：不同磨损程度的切削齿均能达到岩石的破坏极限，均可以有效地进行破岩，但对比预破碎面积和应力极值可知，未磨损齿的大于磨损齿的，表明破岩过程中未磨损齿在相同的模拟条件下可以破碎更多体积的岩石，即机械比能更低。这也与后续的切削热分析形成呼应，随着切削齿磨损高度的增加，与岩石的接触面积增大，致使磨损齿的破岩能力削弱，摩擦生热能力增强。
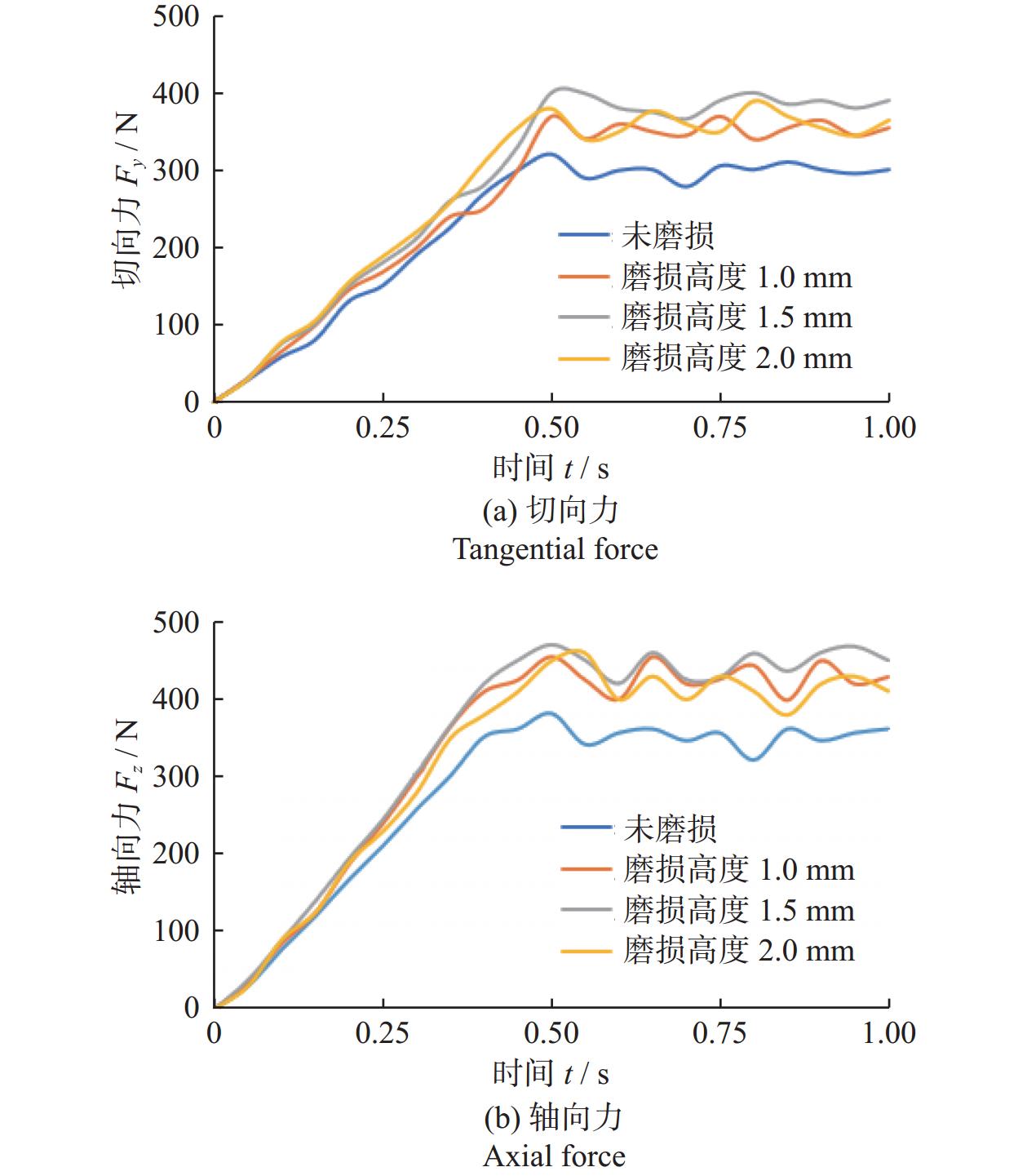
图 4 切削齿切削破碎岩石应力场分布特征Figure 4. Distribution characteristics of stress field in cutting broken rock with wear teeth2.2 磨损高度对切削载荷的影响
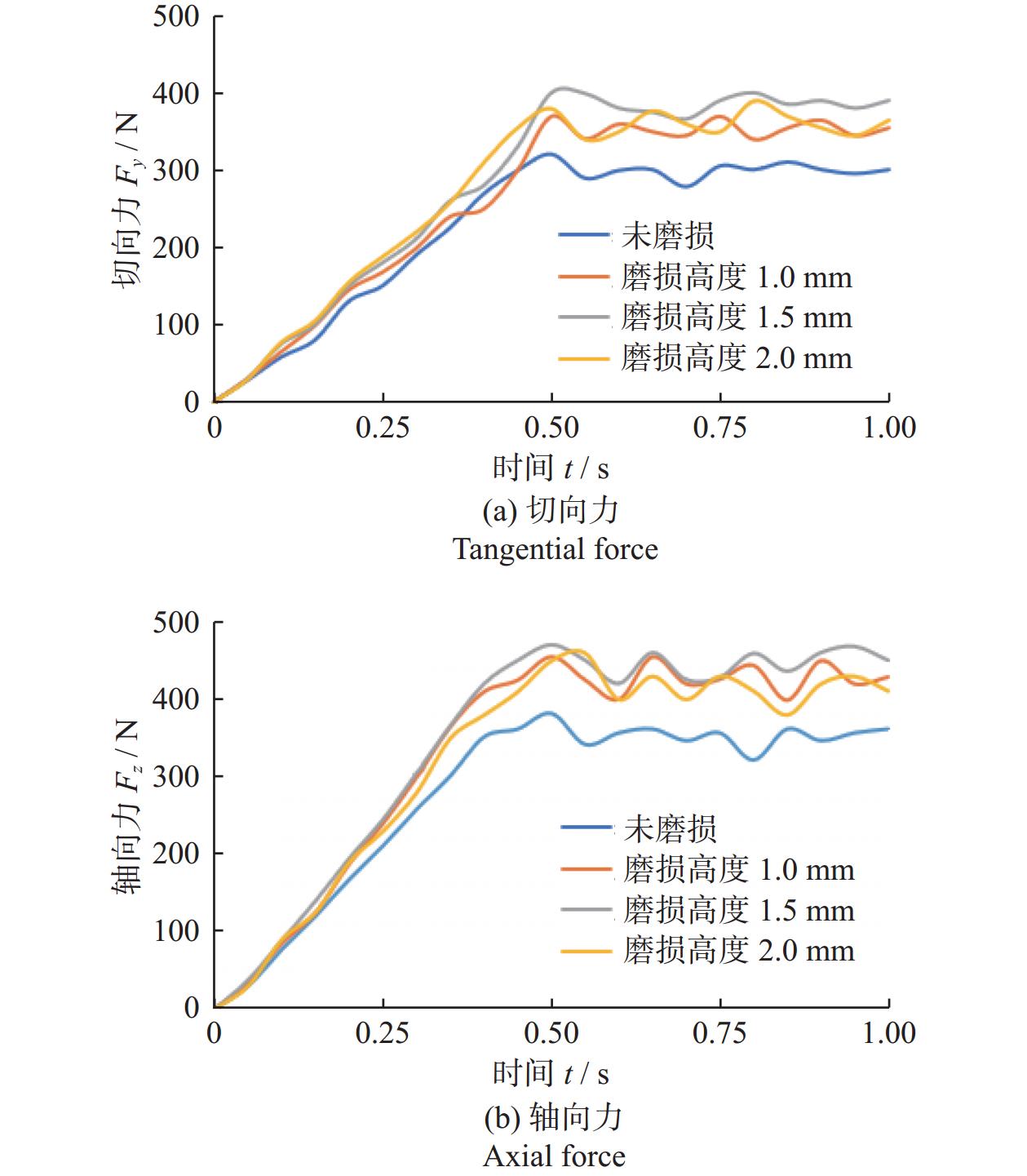
在模拟条件（前倾角15°、切削深度1.5 mm）下，切削载荷的大小和波动程度在磨损高度为0～1.5 mm时，随磨损高度的增加而增大，在磨损高度＞1.5 mm时，会有小幅度下降，如图5所示。切向力方面，磨损高度1.5 mm的切削齿受到的切向力最大，但当磨损高度为2.0 mm时，切向力有所回落。这是因为切削齿严重磨损会使切削面积增大，切削齿与岩石是面接触，齿刃锋利度受损，切削齿难以吃入岩石[18]。轴向力方面，磨损齿的轴向力整体高于未磨损齿的，在磨损高度为0～1.5 mm时，随着磨损高度的增加，轴向力逐渐增大，在磨损高度为1.5 mm时，轴向力达到最大，在磨损高度＞1.5 mm后，轴向力会有所下降。磨损高度1.0 mm与磨损高度2.0 mm的切削齿轴向力恰好均为未磨损齿轴向力的1.2倍，磨损高度1.5 mm的切削齿轴向力是未磨损齿轴向力的1.3倍。
2.3 切削深度对切削载荷的影响
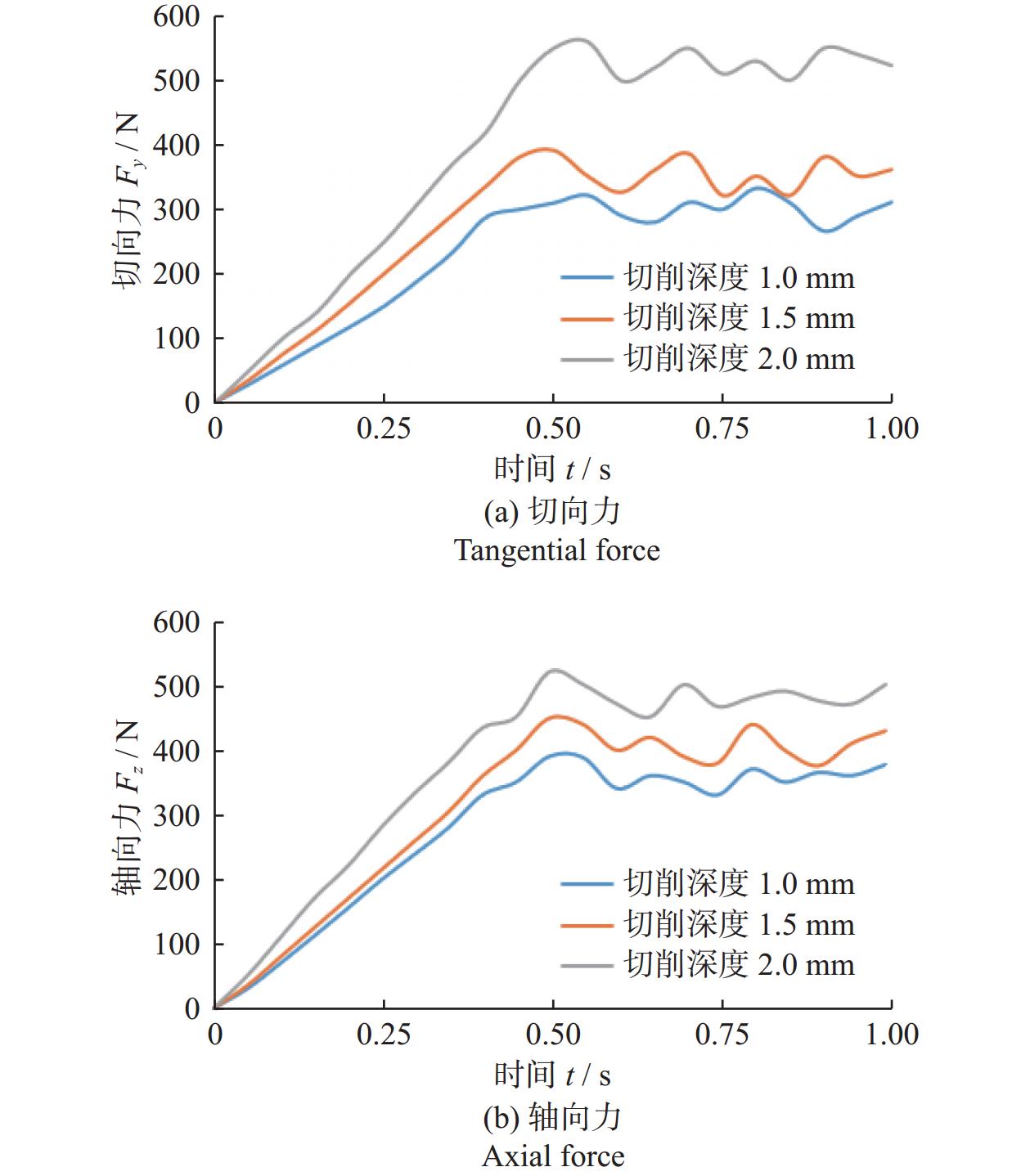
由图6所示，在模拟条件（磨损高度1.0 mm、前倾角15°）下，随着切削深度的增加，切向力和轴向力都逐渐增加，且波动程度更加剧烈。这是因为在小切削深度的条件下，岩石的体积破碎效果较差、破碎成块率低、粉碎率较高，切削载荷波动较小。切向力方面，切削深度2.0 mm的磨损齿切向力为切削深度1.0 mm的磨损齿切向力的1.9倍，增幅较大；切削深度1.5 mm的磨损齿切向力仅比切削深度1.0 mm的磨损齿切向力增加了25%，增幅较小。在轴向力方面，随着切削深度的增加，轴向力的增幅相对比较均衡。
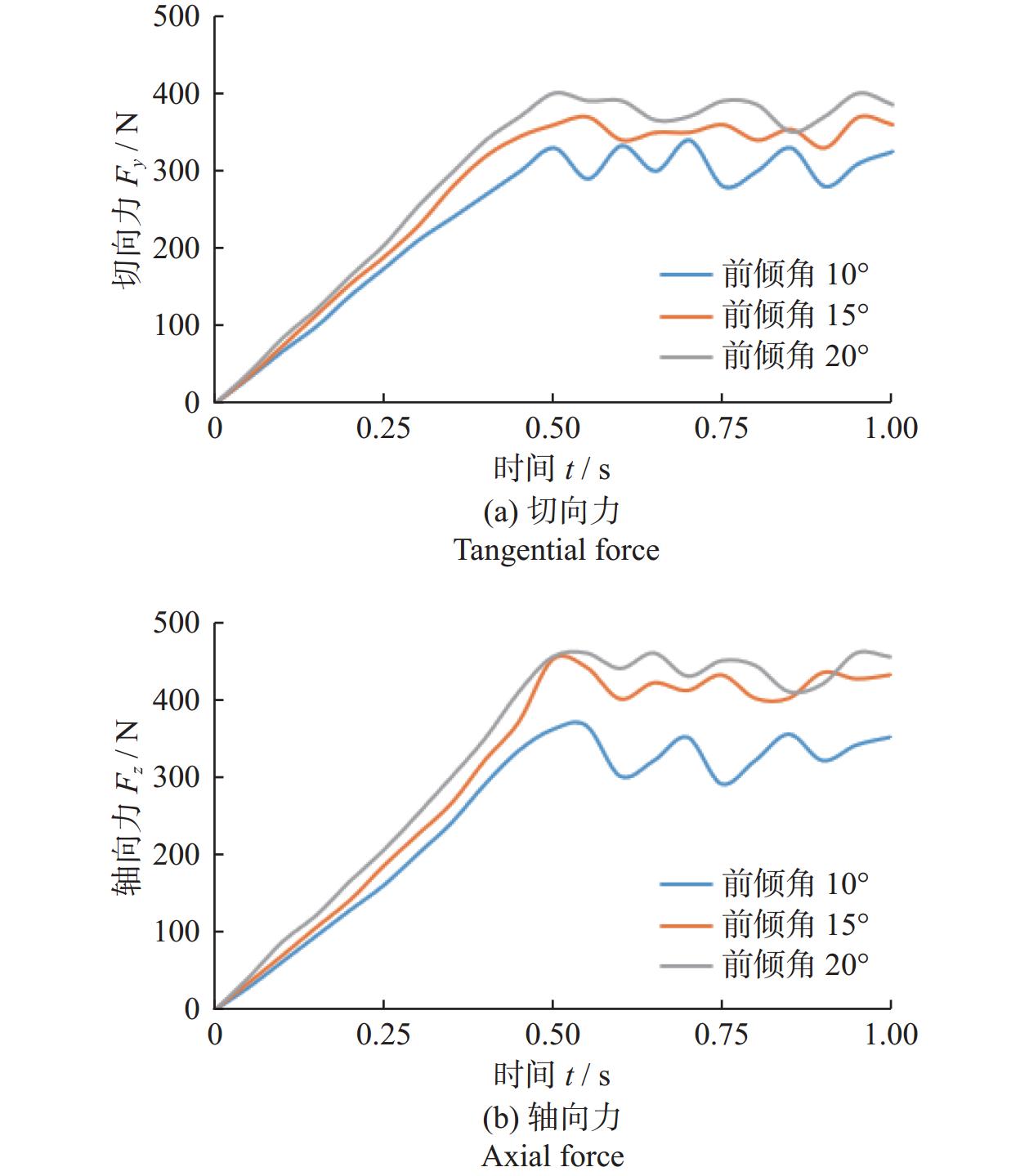
2.4 前倾角对切削载荷的影响
前倾角的确定是PDC钻头设计的重要组成部分，适当的前倾角可以使切削齿刃有效吃入岩石，并具有良好的抗冲击性，直接影响钻头的攻击性与使用寿命。由图7所示，模拟条件（磨损高度1.0 mm、切削深度1.5 mm）下，随着前倾角的增大，磨损齿的切削载荷逐步增加，其中切向力的增幅达到28%，轴向力的增幅达到32%。前倾角为10°时，切削载荷的波动程度比15°和20°前倾角时都更加剧烈。前倾角的设计需要在切削载荷与波动程度上做一定的取舍，如软地层可选取10°～15°的前倾角，使切削齿受到较小的切削载荷；硬地层可以选取15°～20°的前倾角，使切削齿的载荷波动更小，避免加速切削齿磨损和增加冲击载荷，进而延长切削齿的使用寿命。
2.5 磨损高度对切削热的影响
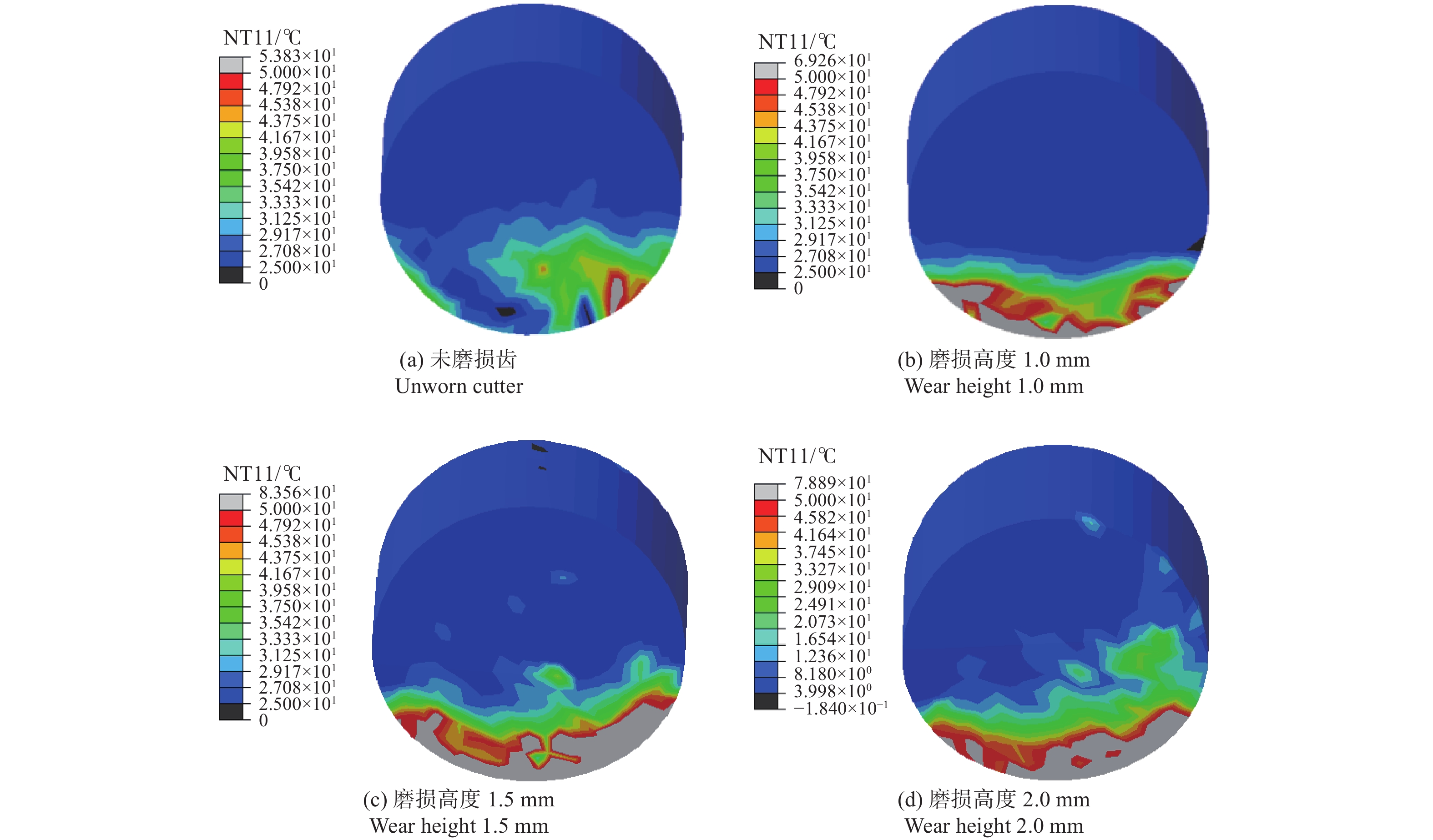
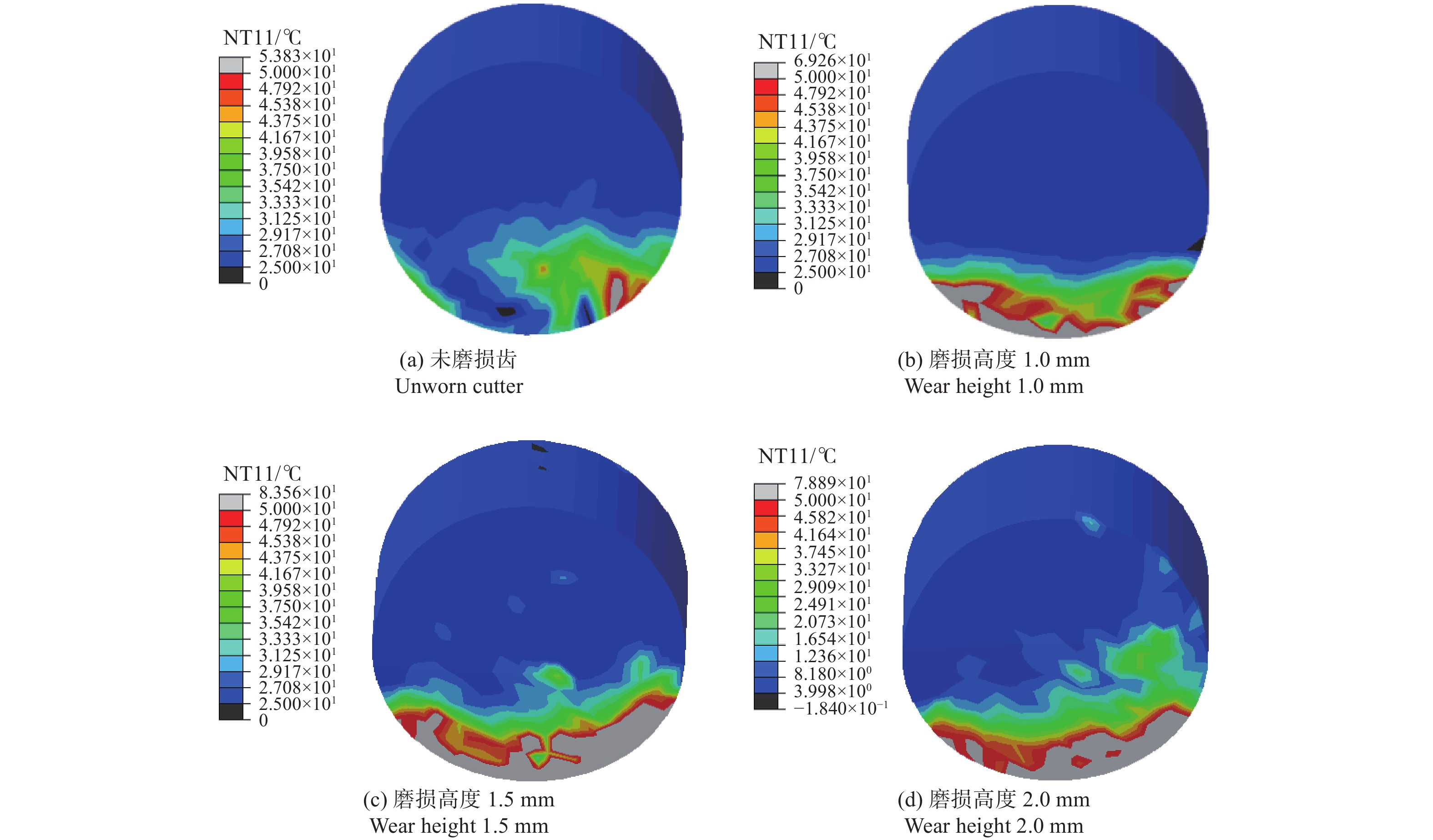
PDC切削齿与岩石相互作用过程中产生的切削热主要来源于切削齿与岩石接触的摩擦生热和岩石自身受压受剪的变形[19]。由图8切削齿温度云图可知，由于切削齿绕中心轴旋转破岩，切削刃各处的线速度不同，远离中心轴一侧的温度会高于靠近中心轴一侧的温度。随着磨损程度的增加，切削齿的温升也更显著，且高温区集中在塑性变形和摩擦生热集中的岩屑-切削齿接触区域。
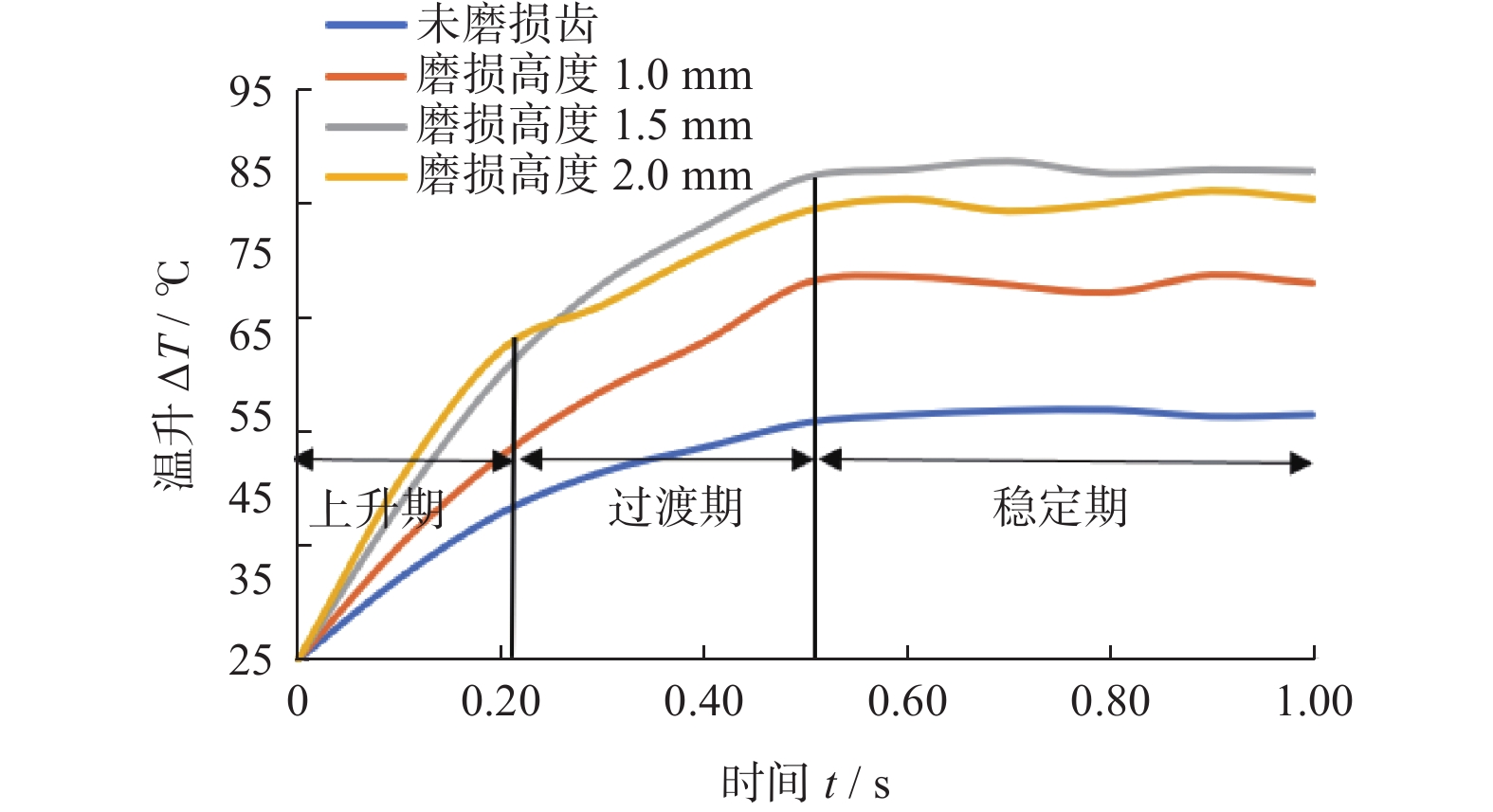
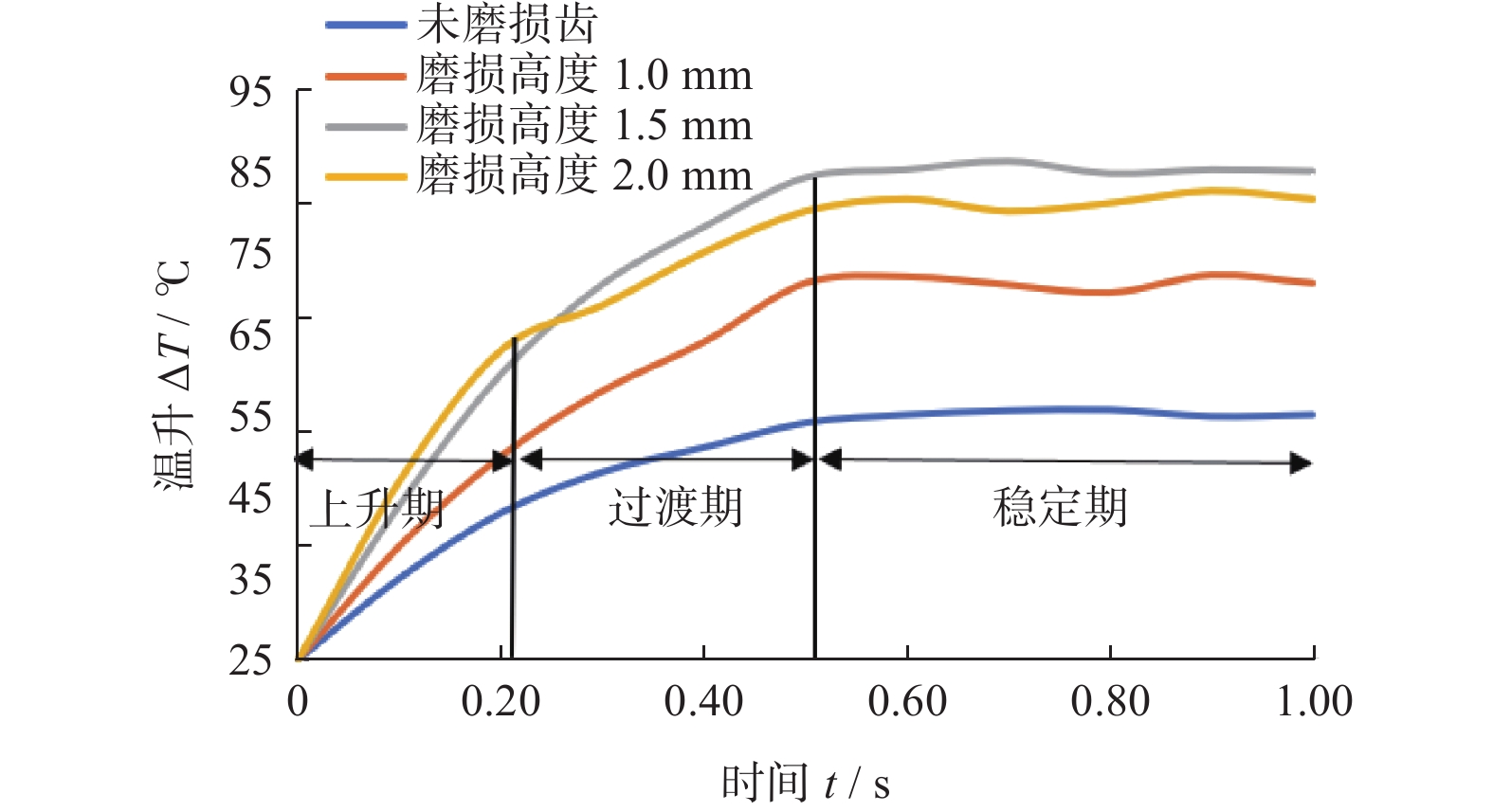
由图9可知温度变化曲线可分为3个阶段：上升期、过渡期与稳定期。随着时间的推进，切削齿的温度持续上升，上升期温升速率大于过渡期，进入稳定期后趋于平缓。出现这种情况的原因是切削齿达到最高温度后，产生的温度与对流换热和热辐射损失的热量相当；磨损齿在破岩过程中的温升远大于未磨损齿的，温度提升54%～103%。因为切削齿在旋切过程中，磨损齿与地层接触的切削弧长和切削面积比未磨损齿更大，其温升显著高于未磨损齿。所以在实际工作中，要及时更换磨损严重的切削齿，让切削齿处于温升速率较低的工作环境，弱化切削热对齿的热磨损，延长PDC钻头的使用寿命。
3. 结论
（1）随着切削深度的增加，切削载荷逐渐变大，且切向力的增幅最大能达到轴向力增幅的2倍，说明磨损过度的切削齿受力更加复杂多变，切削齿的疲劳失效风险增加。在布齿方面，可以考虑在主切削单元PDC的后方放置辅助切削单元，并且让其出露高度低于PDC，这样可以有效减少主切削齿的载荷，降低切削齿发生过载损坏的概率。
（2）磨损齿的切削载荷随着前倾角的增加而增大，前倾角为10°～15°时，切削载荷的波动程度大于前倾角为15°～20°时的波动程度。在综合考虑切削效率与载荷波动的情况下，尽量把前倾角控制在15°～20°，有利于延长切削齿的使用寿命。
（3）伴随磨损高度的增加，切削载荷在磨损高度为1.5 mm（切削齿直径13.4 mm、总高8 mm）时达到最大，较大的切削载荷引起切削齿的振荡，对井下钻具的使用造成影响。切削齿磨损后，其吃入岩石的能力减弱，岩石预破碎面积也有所减少，切削岩石的方式由剪切破坏逐步向挤压破坏过渡，极大地降低了切削齿的破岩效率。
（4）切削破岩过程中，磨损齿的温升远大于未磨损齿的，在模拟条件中可提高54%～103%。在磨损高度为0～1.5 mm时，切削齿的温升随磨损程度的增加而变大，在磨损高度＞1.5 mm时，温升会有小幅度回落，因此切削齿在磨损后热磨损会持续加剧，从而加速切削齿的磨损与失效。在后续的切削过程中，可以选择耐磨、耐高温材料的切削齿，降低钻进的钻压与转速的同时增加泵的水功率等，从而有效抑制热磨损。
-
图 3 PDC切削齿破岩数值模拟模型
Figure 3. Numerical simulation model of rock breaking for PDC cutter
图 4 切削齿切削破碎岩石应力场分布特征
Figure 4. Distribution characteristics of stress field in cutting broken rock with wear teeth
表 1 PDC切削齿和岩石的参数
Table 1. Parameters of PDC cutters and rocks
材 料 PDC 岩石 密度ρ / (kg·m−3) 3 510 2 580 弹性模量 E / GPa 890 25 泊松比 ν 0.077 0.150 热传导率 λ /（W·m−1·℃−1） 543.0 3.5 比热容 c /(J·kg−1·℃−1) 790 800 热膨胀系数 α / ℃−1 2.5 × 10−6 12.0 × 10−6 内摩擦角 φ / (°) — 42 抗压强度 σ bc/ MPa — 40 
下载: 导出CSV
表 2 切削齿破岩仿真方案
Table 2. Simulation scheme of cutter rock breaking
仿真方案 仿真参数 磨损高度 H / mm 前倾角 θ / (°) 切削深度 dDOC / mm 方案一 0、1.0、1.5、2.0 15 1.5 方案二 1.0 10、15、20 1.5 方案三 1.0 15 1.0、1.5、2.0
下载: 导出CSV
-
[1] 刘维, 高德利. PDC钻头研究现状与发展趋势 [J]. 前瞻科技,2023,2(2):168-178. doi: 10.3981/j.issn.2097-0781.2023.02.013LIU Wei, GAO Deli. Research status and development trends of polycrystalline diamond compact bits [J]. Prospect Science and Technology,2023,2(2):168-178. doi: 10.3981/j.issn.2097-0781.2023.02.013 [2] 苏义脑, 路保平, 刘岩生, 等. 中国陆上深井超深井钻完井技术现状及攻关建议 [J]. 石油钻采工艺,2020,42(5):527-542. doi: 10.13639/j.odpt.2020.05.001SU Yinao, LU Baoping, LIU Yansheng, et al. Status and research suggestions on the drilling and completion technologies for onshore deep and ultra deep wells in China [J]. Oil Drilling & Production Technology,2020,42(5):527-542. doi: 10.13639/j.odpt.2020.05.001 [3] 张富晓, 黄志强, 周已. PDC钻头切削齿失效分析 [J]. 石油矿场机械,2015,44(9):44-49. doi: 10.3969/j.issn.1001-3482.2015.09.011ZHANG Fuxiao, HUANG Zhiqiang, ZHOU Yi. Failure analysis of PDC bit cutter [J]. Oil Field Equipment,2015,44(9):44-49. doi: 10.3969/j.issn.1001-3482.2015.09.011 [4] 邓敏凯, 伍开松, 胡伟. PDC钻头切削齿破岩仿真与试验分析 [J]. 石油机械,2014,42(1):10-13. doi: 10.3969/j.issn.1001-4578.2014.01.003DENG Minkai, WU Kaisong, HU Wei. Rock-breaking simulation and experimental analysis of PDC bit cutter [J]. China Petroleum Machinery,2014,42(1):10-13. doi: 10.3969/j.issn.1001-4578.2014.01.003 [5] 祝效华, 李海. PDC切削齿破岩效率数值模拟研究 [J]. 应用基础与工程科学学报,2015,23(1):182-191. doi: 10.16058/j.issn.1005-0930.2015.01.017ZHU Xiaohua, LI Hai. Numerical simulation on mechanical special energy of PDC cutter rock-cutting [J]. Journal of Basic Science and Engineering,2015,23(1):182-191. doi: 10.16058/j.issn.1005-0930.2015.01.017 [6] 杨迎新, 谢松, 蔡灿, 等. PDC磨损齿切削破岩过程的实验研究 [J]. 西南石油大学学报(自然科学版),2023,45(1):180-188. doi: 10.11885/j.issn.1674-5086.2020.06.04.03YANG Yingxin, XIE Song, CAI Can, et al. A study on the mechanism and heat generation law of PDC wear tooth cutting [J]. Journal of Southwest Petroleum University (Science & Technology Edition),2023,45(1):180-188. doi: 10.11885/j.issn.1674-5086.2020.06.04.03 [7] 赵润琦, 陈振良, 史怀忠, 等. 斧形PDC齿破碎致密硬质砂岩特性数值模拟研究 [J]. 石油机械,2021,49(10):8-16. doi: 10.16082/j.cnki.issn.1001-4578.2021.10.002ZHAO Runqi, CHEN Zhenliang, SHI Huaizhong, et al. Numerical simulation study on characteristics of tight hard sand broken by axe-shaped PDC cutter [J]. China Petroleum Machinery,2021,49(10):8-16. doi: 10.16082/j.cnki.issn.1001-4578.2021.10.002 [8] 张春亮, 王锦成, 柯晓华, 等. 磨损齿PDC钻头的切削性能试验 [J]. 金刚石与磨料磨具工程,2023,43(1):35-42. doi: 10.13394/j.cnki.jgszz.2022.0084ZHANG Chunliang, WANG Jincheng, KE Xiaohua, et al. Experimental study on working mechanics of PDC bit with worn teeth [J]. Diamond & Abrasives Engineering,2023,43(1):35-42. doi: 10.13394/j.cnki.jgszz.2022.0084 [9] ROSTAMSOWLAT I, AKBARI B, EVANS B. Analysis of rock cutting process with a blunt PDC cutter under different wear flat inclination angles [J]. Journal of Petroleum Science and Engineering,2018,171:771-783. doi: 10.1016/j.petrol.2018.06.003 [10] 朱光辉, 况雨春, 林伟. PDC磨损齿切削载荷与生热规律研究 [J]. 石油机械,2021,49(5):68-73. doi: 10.16082/j.cnki.issn.1001-4578.2021.05.010ZHU Guanghui, KUANG Yuchun, LIN Wei. Research on cutting load and heat generation law of PDC wearing cutter [J]. China Petroleum Machinery,2021,49(5):68-73. doi: 10.16082/j.cnki.issn.1001-4578.2021.05.010 [11] VORONTSOV A L, SULTAN-ZADE N M, ALBAGACHIEV A Y, et al. Development of a new theory of thermal cutting processes 3. Influence of cutter's front angle on the cutting temperature and influence of preheating of the blank on the cutting force [J]. Russian Engineering Research,2010,30(3):274-275. doi: 10.3103/S1068798X10030159 [12] 邓嵘, 李勇. PDC钻头切削齿破岩温度场有限元仿真分析 [J]. 石油机械,2012,40(12):37-42.DENG Rong, LI Yong. Simulation analysis of temperature field for PDC bit cutter rock breaking [J]. China Petroleum Machinery,2012,40(12):37-42. [13] MAMALIS A G, HORVÁTH M, BRANIS A S, et al. Finite element simulation of chip formation in orthogonal metal cutting [J]. Journal of Materials Processing Technology,2001,110(1):19-27. doi: 10.1016/S0924-0136(00)00861-X [14] 张在兴, 周琴, 张凯, 等. 切削角度对切削齿温度分布的影响分析 [J]. 石油机械,2021,49(12):17-26. doi: 10.16082/j.cnki.issn.1001-4578.2021.12.003ZHANG Zaixing, ZHOU Qin, ZHANG Kai, et al. Analysis of effect of cutting angle on temperature distribution of cutting gear [J]. China Petroleum Machinery,2021,49(12):17-26. doi: 10.16082/j.cnki.issn.1001-4578.2021.12.003 [15] 邓楚键, 何国杰, 郑颖人. 基于M-C准则的D-P系列准则在岩土工程中的应用研究 [J]. 岩土工程学报,2006,28(6):735-739. doi: 10.3321/j.issn:1000-4548.2006.06.011DENG Chujian, HE Guojie, ZHENG Yingren. Studies on Drucker-Prager yield criterions based on M-C yield criterion and application in geotechnical engineering [J]. Chinese Journal of Geotechnical Engineering,2006,28(6):735-739. doi: 10.3321/j.issn:1000-4548.2006.06.011 [16] 袁小平, 刘红岩, 王志乔. 基于Drucker-Prager准则的岩石弹塑性损伤本构模型研究 [J]. 岩土力学,2012,33(4):1103-1108. doi: 10.3969/j.issn.1000-7598.2012.04.021YUAN Xiaoping, LIU Hongyan, WANG Zhiqiao. Study of elastoplastic damage constitutive model of rocks based on Drucker-Prager criterion [J]. Rock and Soil Mechanics,2012,33(4):1103-1108. doi: 10.3969/j.issn.1000-7598.2012.04.021 [17] CHEN S L, KHLEFAT Y, CLEBOSKI C, et al. A new method of backup-cutter layout to extend bit life without sacrificing rate of penetration [J]. SPE Drilling & Completion,2018,33(2):115-129. doi: 10.2118/187644-PAArticlehistory [18] 梁尔国, 李子丰, 邹德永. PDC切削齿受力的试验研究 [J]. 石油机械,2009,37(11):12-15.LIANG Erguo, LI Zifeng, ZOU Deyong. Experimental study on force of PDC cutter [J]. China Petroleum Machinery,2009,37(11):12-15. [19] 李勇. PDC钻头切削齿破岩过程热分析与仿真[D]. 成都: 西南石油大学, 2012.LI Yong. Thermal analysis and simulation of rock breaking process of PDC bit cutter [D]. Chengdu: Southwest Petroleum University, 2012. -
下载:
点击查看大图
计量
- 文章访问数: 561
- HTML全文浏览量: 280
- PDF下载量: 18
- 被引次数: 0
邮件订阅
RSS
