Prediction and optimization of robot processing technology based on neural network and genetic algorithm
-
摘要: 以KUKA KR60L30HA型工业机器人加工砂岩为例,基于BP神经网络和遗传算法进行机器人加工磨削力的预测和磨削工艺参数的优化。首先,采用正交试验法,分析加工工艺参数对磨削力信号的影响规律;其次,采用BP神经网络进行机器人加工磨削力预测模型训练并进行预测;最后,采用遗传算法对磨削加工工艺参数进行优化。结果表明:磨削工艺参数对3个磨削力分量和磨削合力的影响主次顺序不同,基本上都随径向切深ae、轴向切深ap、进给速度vw的增加呈增长趋势,随主轴转速n的增加呈下降趋势;基于BP神经网络建立的预测模型具有较好的预测精度和稳定性,符合预测要求;同时,采用遗传算法得到的优化磨削工艺参数组合是ae = 2.28 mm,ap = 2.98 mm,n = 9 586.65 r/min,vw = 2 207.67 mm/min,此时的材料去除率预测值RMRRP = 14 999.79 mm3/min,材料去除率试验值RMRRT = 14 194.44 mm3/min,试验值相对预测值的相对误差为−5.37%。Abstract:
Objectives With the rapid development of industrial automation and intelligent manufacturing, the application of industrial robots in the stone processing industry has garnered increasing attention. However, compared to other advanced manufacturing sectors, the mechanization, automation and intelligence of the stone processing industry remain relatively underdeveloped. This study aims to explore the optimal processing methods for stone industrial robots' grinding operations using BP neural networks and genetic algorithms, taking the processing of sandstone as an example. Methods Taking the KUKA KR60L30HA industrial robot equipped with a brazed flat grinding head as the representative, the effects of different grinding process parameters on grinding force signals were systematically analyzed by the orthogonal test method. Firstly, the grinding force signal data were collected using different grinding test settings. Subsequently, a three-layer grinding force prediction model based on a BP neural network was established, and linear regression analysis was conducted using the orthogonal experimental data as samples to compare the predicted values with the experimental values. Finally, the genetic algorithm was applied to optimize grinding process parameters with material removal rates as the indicator. Results The grinding process parameters have significant effects on grinding forces, but the order of major and secondary effects of different parameters varies with grinding force components. The order of influence on tangential grinding force is the axial cutting depth ap, followed by radial cutting depth ae, the feed rate vw and the spindle speed n, while the order of influence on normal grinding force is ap, vw, ae and n. In contrast, the order of influence of axial grinding force is n, ae, vw and ap, while the total grinding force is most affected by vw, in the order of vw, ae, n and ap. Additionally, all components of grinding force generally increase with the rise of ae, ap and vw, and decrease with the increase of spindle speed n. As the radial cutting depth ae increases, the ratio of normal to tangential grinding force shows a continuous downward trend. As the axial cutting depth ap increases, the grinding force ratio fluctuates within a certain range. As the spindle speed n increases, the grinding force ratio first increases, then decreases, and then slightly increases. When the feed rate vw increases, the grinding force ratio shows an initial decrease followed by an increasing trend. After training and predicting using the BP neural network model, the predicted values of tangential, normal and axial grinding forces are compared with the experimental data. The maximum absolute relative error of the axial grinding force is 7.84%, and the correlation coefficient of the model is as high as 0.998 09, indicating significant prediction accuracy of the mpdel. The optimal process parameter combination determined through genetic algorithm optimization is a radial cutting depth of 2.28 mm, an axial cutting depth of 2.98 mm, a spindle speed of 9 586.65 r/min and a feed rate of 2 207.67 mm/min. Under the optimal process parameter combination, the predicted material removal rate of the workpiece is 14 999.79 mm3/min, with a relative error of −5.37% compared to the actual experimental value of 14 194.44 mm3/min. This further demonstrates the effectiveness of the proposed optimization strategy. Conclusions The constructed grinding force prediction and process parameter optimization model has achieved systematic analysis and optimization of grinding force in robot sandstone processing. This model can clearly reveal the role of various grinding process parameters in machining and reflect their importance in improving machining efficiency and material removal rate. The changing trend of grinding force varies with different processing conditions, and there are significant differences in the influences of different parameter combinations on grinding forces, especially the influences of axial cutting depth and the feed rate, which are particularly significant. The optimal process parameter combination for material removal rate in stone processing is determined through BP neural network and genetic algorithm, and the relative error between the predicted value and the experimental value is relatively small. -
石材作为一种高档建筑装饰材料广泛应用于室内外装饰设计、幕墙装饰和公共设施建设中。但石材的加工存在粉尘多、噪声大、污染严重等[1-2]问题,且相较于其他先进制造业,石材加工产业的机械化、自动化、智能化程度相对落后。随着“中国制造2025”的推进,国家、地方政府和行业制订了一系列法规政策及标准,投入人力、物力和财力以推动石材加工产业的转型升级。随着石材加工产业从半机械化、半自动化加工向自动化、数字化、智能化方向发展,数控加工机床、多轴雕刻机得到了广泛应用,且五轴加工中心、工业机器人加工系统也得到了一定的推广及应用。其中的工业机器人加工系统因其高度的灵活性和可加工范围大等特点,在大型加工件的加工中得到了应用,也在立体石雕行业得到了认可[3]。
与数控机床相比,工业机器人串联结构的刚度较低,但其在大型加工件中的应用具有不可替代的优势,已成为近年来的研究热点。工业机器人的加工研究主要集中在加工能耗[4-5]、加工颤振[6-8]、砂带磨削[9-12]、磨抛[13-15]等方向,且其加工对象多为金属材料,以石材为加工对象的研究相对较少。文献[16]采用固定的磨削工艺参数,对工业机器人持续磨削花岗岩过程中的磨削力和工具磨损进行了跟踪研究。文献[17]以减小精加工过程中的磨削力波动为约束,对工业机器人加工大理石的路径进行了规划。上述研究从不同角度进行了工业机器人加工石材的磨削力研究,但未从整体出发对不同磨削加工工艺参数下磨削力信号的变化规律及其影响因素进行分析。
因此,对工业机器人加工砂岩的磨削力信号进行分析,探究加工工艺参数对不同加工方向磨削力信号的影响规律;进一步利用BP神经网络建立磨削力预测模型,并基于遗传算法以磨削力为约束条件、材料去除率为目标函数,进行磨削加工工艺参数优化,以期实现石材的工业机器人最优加工。
1. 试验方案
1.1 试验系统
试验在由KUKA KR60L30HA型工业机器人(负载为60 kg,电主轴最高转速为10 000 r/min)及其他部件组成的机器人石雕加工系统上进行,如图1所示。
试验采用的工具是直径d = 15.8 mm的钎焊金刚石平底磨头,其磨削刃长度为30 mm,悬伸长度为50 mm。金刚石磨粒粒度标记为40/45,磨粒浓度为3.38颗/mm2,磨粒出露高度为160.54 μm。试验工件是长、宽均为200 mm的绿砂岩,其抗压强度为25 MPa,抗拉强度为1.71 MPa,肖氏硬度为46,沿着y轴从正方向向负方向加工。工件装夹后固定在Kistler 9255B型测力仪上。
加工时的磨削力信号采用Kistler 9255B型测力仪、5080型放大器和5697数据采集器进行采集,采样频率为10 kHz。9255B型测力仪x、y、z 3个方向的量程分别为±20 kN、±20 kN、−10~40 kN。
1.2 正交试验设计
通过L25(54)正交试验表设计4因素5水平正交试验,选取的磨削参数为主轴转速n、进给速度vw、径向切深ae、轴向切深ap。磨削力的正交试验因素及水平如表1所示。
表 1 磨削力的正交试验因素及水平Table 1. Orthogonal test factors and levels of grinding force水平 因素 径向切深
ae / mm
A轴向切深
ap / mm
B主轴转速
n / (r·min−1)
C进给速度
vw / ( mm·min−1)
D1 2 1.0 5 000 500 2 3 1.5 6 000 1 000 3 4 2.0 7 000 1 500 4 5 2.5 8 000 2 000 5 6 3.0 9 000 2 500 2. 试验结果与讨论
2.1 磨削力正交试验结果
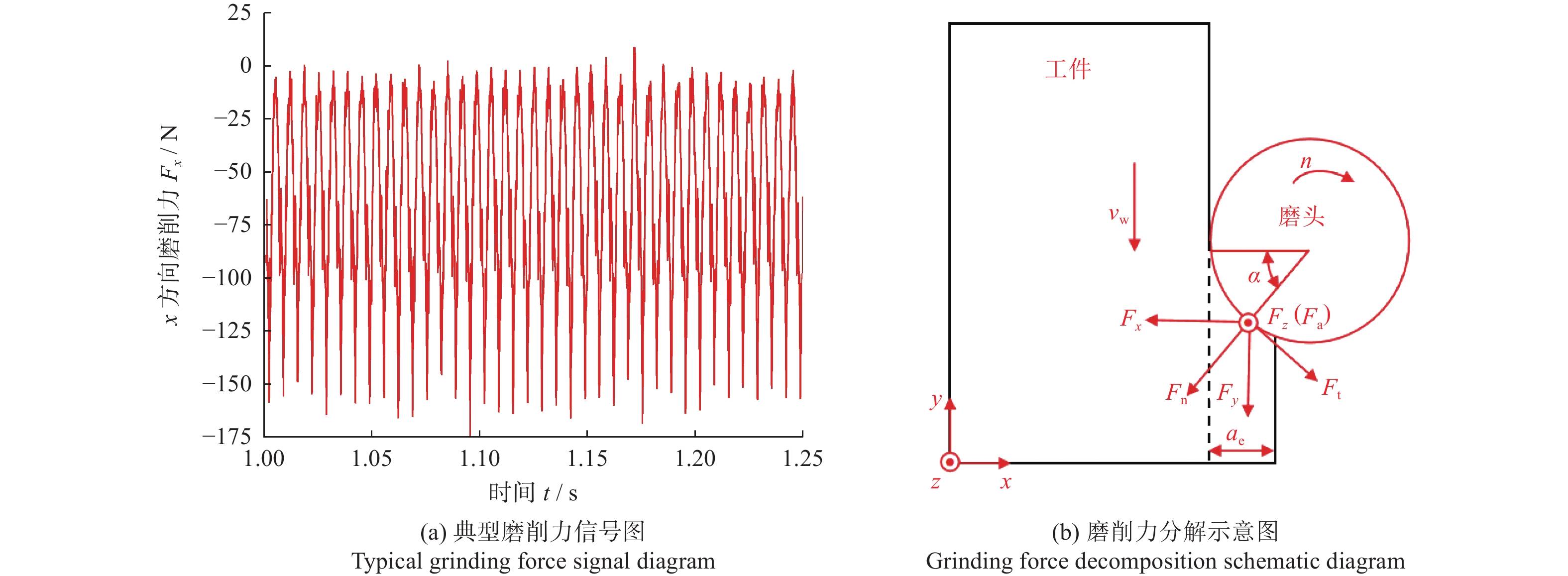
在表1的条件下对砂岩工件进行铣削,将获得的原始磨削力信号导入软件中进行数据处理,x方向的磨削力原始信号Fx曲线如图2a所示。对原始磨削力信号采用巴特沃斯低通滤波,其频率设置为10 Hz,获得平均磨削力分量Fx、Fy、Fz。为方便进一步分析,将3个磨削力分量按照切向、法向、轴向进行分解,如图2b所示,获得式(1)中的法向、切向和轴向3个磨削分力及磨削合力。
$$\left\{\begin{array}{l} F_{\mathrm{t}}=F_{{x}} \sin \alpha+F_{{y}} \cos \alpha \\ F_{\mathrm{n}}=F_{{x}} \cos \alpha+F_{{y}} \sin \alpha \\ F_{\mathrm{a}}=F_{\textit{z}} \\ F_{合}=\sqrt{F_{\mathrm{t}}^2+F_{\mathrm{n}}^2+F_{\mathrm{a}}^2} \end{array}\right.$$ (1) 式中:α为接触角,$ \alpha ={\mathrm{arccos}}\left(1-\dfrac{2{a}_{{\mathrm{e}}}}{d}\right) $;$F_{合} $为磨削合力;Ft为切向磨削力;Fn为法向磨削力;Fa为轴向磨削力。
磨削力的正交试验数据及极差分析结果如表2所示,表中的法向和切向磨削力比Kf = Fn/Ft,且表中的材料去除率RMRR由式(2)计算,其单位为mm3/min。
表 2 磨削力正交试验数据及极差分析结果Table 2. Orthogonal experimental data and range analysis results of grinding forces序号 A B C D 切向磨削力
Ft / N法向磨削力
Fn / N轴向磨削力
Fa / N磨削合力
F合 / N法向和切向
磨削力比Kf材料去除率
RMRR / (mm3·min−1)1 2 1.0 5 000 500 12.10 12.59 39.83 41.93 1.04 1.00 × 103 2 2 1.5 6 000 1 000 30.89 32.94 49.82 61.79 1.07 3.00 × 103 3 2 2.0 7 000 1 500 32.65 34.93 36.05 53.23 1.07 6.00 × 103 4 2 2.5 8 000 2 000 40.57 43.59 33.32 59.70 1.07 10.00 × 103 5 2 3.0 9 000 2 500 48.55 52.92 11.78 64.44 1.09 15.00 × 103 6 3 1.0 6 000 1 500 16.59 14.83 39.14 42.89 0.89 4.50 × 103 7 3 1.5 7 000 2 000 45.56 40.67 61.57 78.22 0.89 9.00 × 103 8 3 2.0 8 000 2 500 71.34 63.60 73.6 105.57 0.89 15.00 × 103 9 3 2.5 9 000 500 27.15 24.36 20.38 35.11 0.90 3.75 × 103 10 3 3.0 5 000 1 000 64.88 57.65 38.59 79.14 0.89 9.00 × 103 11 4 1.0 7 000 2 500 36.68 38.50 40.87 56.59 1.05 10.00 × 103 12 4 1.5 8 000 500 21.46 17.72 32.41 38.90 0.83 3.00 × 103 13 4 2.0 9 000 1 000 46.78 39.78 51.96 69.92 0.85 8.00 × 103 14 4 2.5 5 000 1 500 121.43 96.06 82.76 147.82 0.79 15.00 × 103 15 4 3.0 6 000 2 000 143.56 108.88 68.30 161.44 0.76 24.00 × 103 16 5 1.0 8 000 1 000 23.37 19.53 39.76 46.38 0.84 5.00 × 103 17 5 1.5 9 000 1 500 48.45 38.67 66.55 82.67 0.80 11.25 × 103 18 5 2.0 5 000 2 000 164.93 119.23 163.9 232.69 0.72 20.00 × 103 19 5 2.5 6 000 2 500 227.37 165.41 151.50 273.57 0.73 31.25 × 103 20 5 3.0 7 000 500 58.23 50.03 38.07 70.97 0.86 7.50 × 103 21 6 1.0 9 000 2 000 34.05 26.80 53.53 64.63 0.79 12.00 × 103 22 6 1.5 5 000 2 500 124.19 80.59 174.40 215.62 0.65 22.50 × 103 23 6 2.0 6 000 500 45.00 45.49 63.48 82.59 1.01 6.00 × 103 24 6 2.5 7 000 1 000 93.31 75.93 75.99 125.78 0.81 15.00 × 103 25 6 3.0 8 000 1 500 146.63 107.90 89.36 177.41 0.74 27.00 × 103 切向
磨削力
Ft / NKi1 32.95 24.56 97.51 32.79 ap > ae > vw > n Ki2 45.10 54.11 92.68 51.84 Ki3 73.98 72.14 53.28 73.15 Ki4 104.47 101.97 60.68 85.73 Ki5 88.64 92.37 41.00 101.63 Ri 71.52 77.41 56.51 68.84 法向
磨削力
Fn / NKi1 35.40 22.45 73.22 30.04 ap > vw > ae > n Ki2 40.22 42.12 73.51 45.17 Ki3 60.19 60.61 48.01 58.48 Ki4 78.58 81.07 50.47 67.83 Ki5 67.34 75.48 36.51 80.20 Ri 43.18 58.62 37.00 50.17 轴向
磨削力
Fa / NKi1 34.16 42.63 99.90 38.83 n > ae > vw > ap Ki2 46.66 76.95 74.45 51.22 Ki3 55.26 77.80 50.51 62.77 Ki4 91.96 72.79 53.69 76.12 Ki5 91.35 49.22 40.84 90.43 Ri 57.80 35.17 59.06 51.60 磨削
合力
F合 / NKi1 56.22 50.48 143.44 53.90 vw > ae > n > ap Ki2 68.18 95.44 124.46 76.60 Ki3 94.93 108.80 76.96 100.80 Ki4 141.26 128.40 85.59 119.33 Ki5 133.21 110.68 63.35 143.16 Ri 85.04 77.91 80.09 89.26 法向和
切向磨
削力比
KfKi1 1.068 0.922 0.819 0.927 ae > n > vw > ap Ki2 0.893 0.846 0.892 0.891 Ki3 0.855 0.909 0.937 0.858 Ki4 0.789 0.861 0.873 0.847 Ki5 0.799 0.866 0.885 0.882 Ri 0.280 0.075 0.119 0.080 $$ {R}_{\mathrm{M}\mathrm{R}\mathrm{R}}={a}_{\mathrm{e}}\times {a}_{\mathrm{p}}\times {v}_{\mathrm{w}} $$ (2) 一般情况下,用Xij(i = A,B,C,D;j = 1,2,3,4,5)表示因素i在j水平下的变量值,Kij表示因素i在j水平下结果的统计参数,可表示为:
$$ K_{i j}=\frac{1}{N} \sum_{n=1}^N Y_{i j n} $$ (3) 式中:N为因素i在j水平的试验组数,Yijn为因素i在j水平下的第n次试验结果。
极差分析用于判断各个因素对试验结果的影响程度,极差Ri计算公式为:
$$ R_i=\max \left\{K_{i j}\right\}-\min \left\{K_{i j}\right\}$$ (4) 2.2 磨削加工工艺参数对磨削力的影响
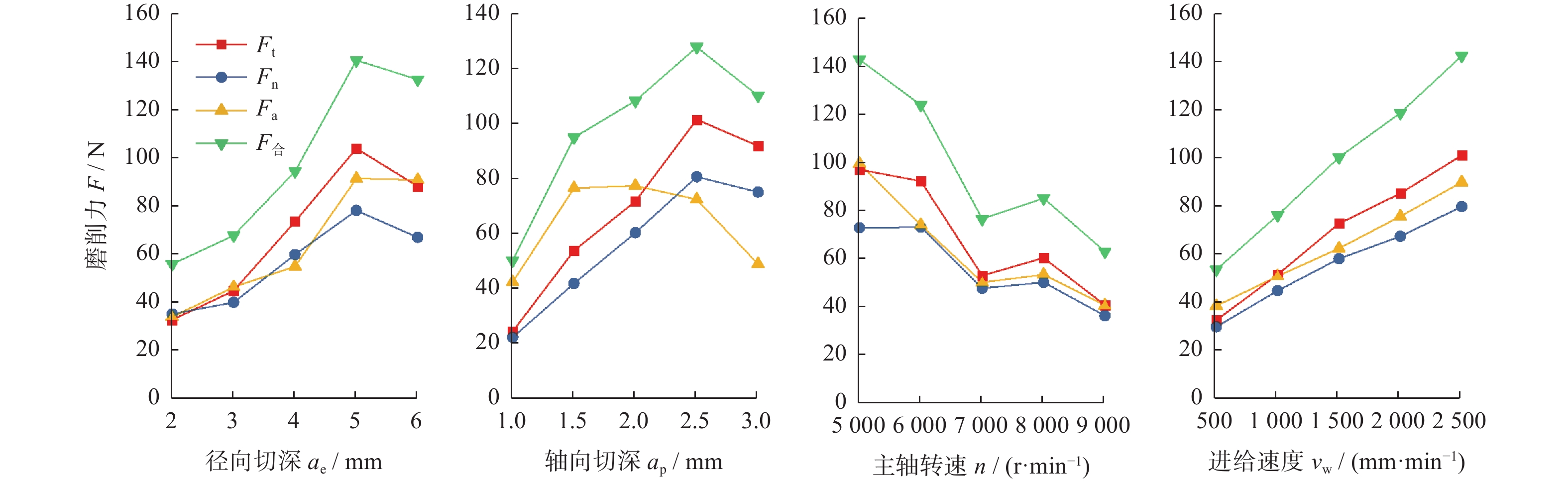
由表2的极差分析结果可知:影响切向磨削力的主次顺序为轴向切深ap、径向切深ae、进给速度vw和主轴转速n;影响法向磨削力的主次顺序为轴向切深ap、进给速度vw、径向切深ae和主轴转速n;影响轴向磨削力的主次顺序为主轴转速n、径向切深ae、进给速度vw和轴向切深ap;影响磨削合力的主次顺序为进给速度vw、径向切深ae、进给速度vw和轴向切深ap。
磨削工艺参数对磨削力的影响规律如图3所示。从图3可知:随着径向切深ae增加,法向、切向、轴向磨削力和磨削合力4个磨削力都呈先增长后略微下降的趋势;随着轴向切深ap增加,切向、法向磨削力和磨削合力都呈先增长后略微下降的趋势,而轴向磨削力呈先上升、再基本稳定、最后下降的趋势;随着主轴转速n增加,4个磨削力都呈下降趋势;随着进给速度vw增加,4个磨削力都呈大幅增长的趋势。
2.3 磨削加工工艺参数对磨削力比的影响
法向和切向磨削力比Kf是用来衡量材料磨削难易程度的重要参量之一,同时也反映了砂轮表面磨粒的锋利度。磨削力比大,以法向磨削力的压溃作用为主来去除材料;磨削力比小,以切向磨削力为主来去除材料。
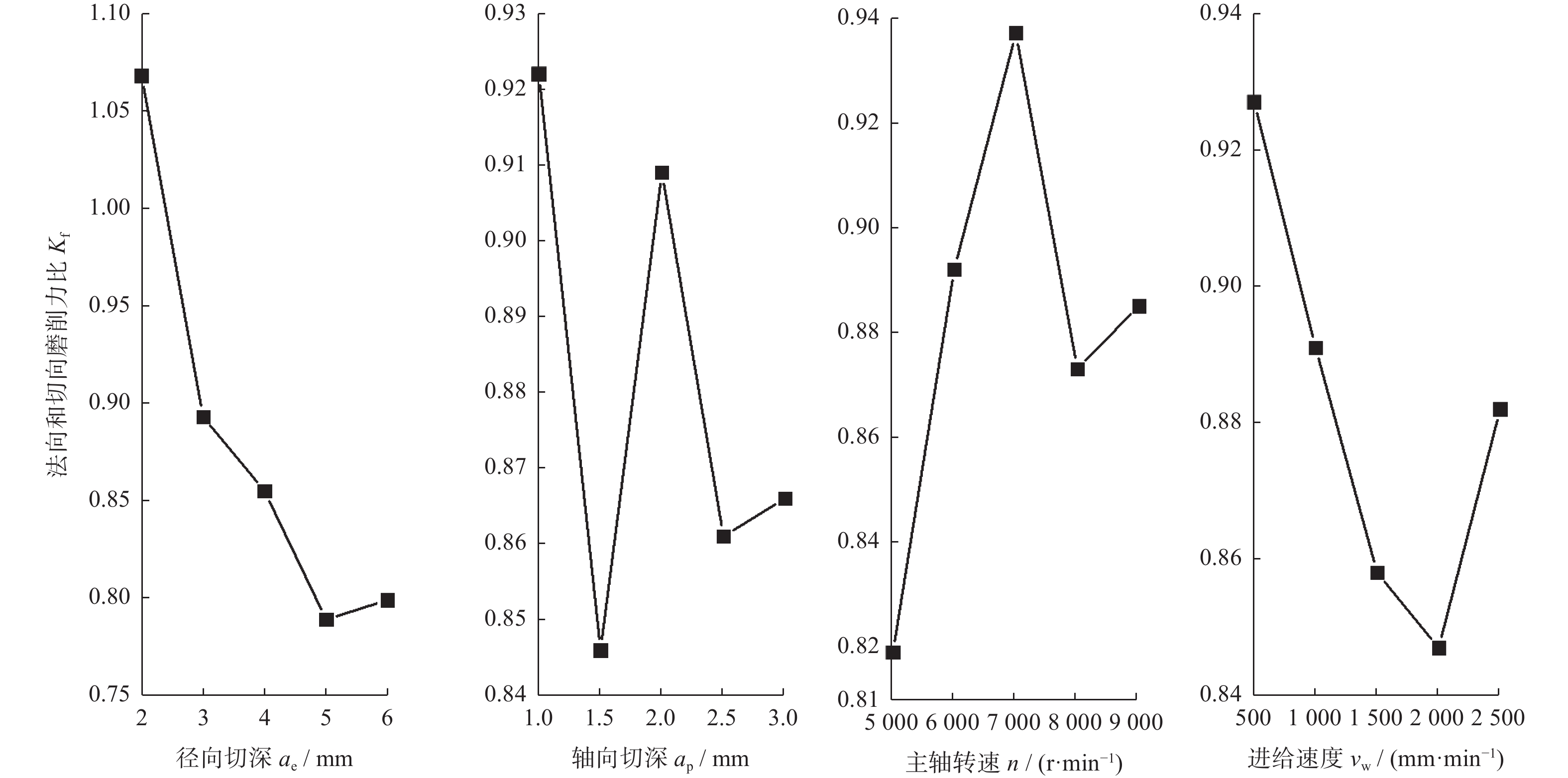
由表2可知:磨削力比Kf最大值为1.09(试验序号为5,各参数是ae = 2 mm,ap = 3.0 mm,n = 9 000 r/min,vw = 2 500 mm/min),此时的材料去除以法向磨削力为主;最小值为0.65(试验序号为22,各参数是ae = 6 mm,ap = 1.5 mm;n =
5000 r/min,vw = 2 500 mm/min),此时的材料去除以切向磨削力为主。磨削加工工艺参数对磨削力比影响的主次顺序为径向切深ae、主轴转速n、进给速度vw和轴向切深ap。磨削工艺参数对磨削力比的影响规律如图4所示。由图4可知:随着径向切深ae增加,磨削力比呈下降趋势;随着轴向切深ap增加,磨削力比在一定范围内波动;随着主轴转速n增加,磨削力比呈先上升、后下降、再小幅上升趋势;随着进给速度vw增加,磨削力比呈先下降、后上升趋势。
2.4 BP神经网络磨削力预测模型构建
BP神经网络是一种广泛运用于识别、回归等领域的神经网络,是一种按误差逆向传播算法训练的神经网络;其包含输入层、隐含层、输出层,而隐含层的层数会影响预测精度,通过调整隐含层的神经元节点数可以实现任意非线性变化的映射[18]。为此,构建由输入层、隐含层和输出层组成的3层网络,来建立机器人加工的磨削力预测模型。模型中隐含层的节点数由经验公式确定[19]:
$$ M = \sqrt {e + m} + a $$ (5) 式中:M为隐含层的节点数;e为输入层节点数,e = 4;m为输出层节点数,m = 4;a为[1, 10]的常数。
根据式(5)可计算出M的取值范围为4~12,在该范围内对M取整数值进行训练。当M = 12时,训练的效率和精度均最佳。因此,本文取M = 12。
选取表2的25组正交试验数据为训练样本,来构建BP神经网络磨削力预测模型,其学习率为0.1。模型中的传递函数设置是:输入层至隐含层为tansig函数,隐含层至输出层为purelin函数,训练函数为traingdm函数[20]。
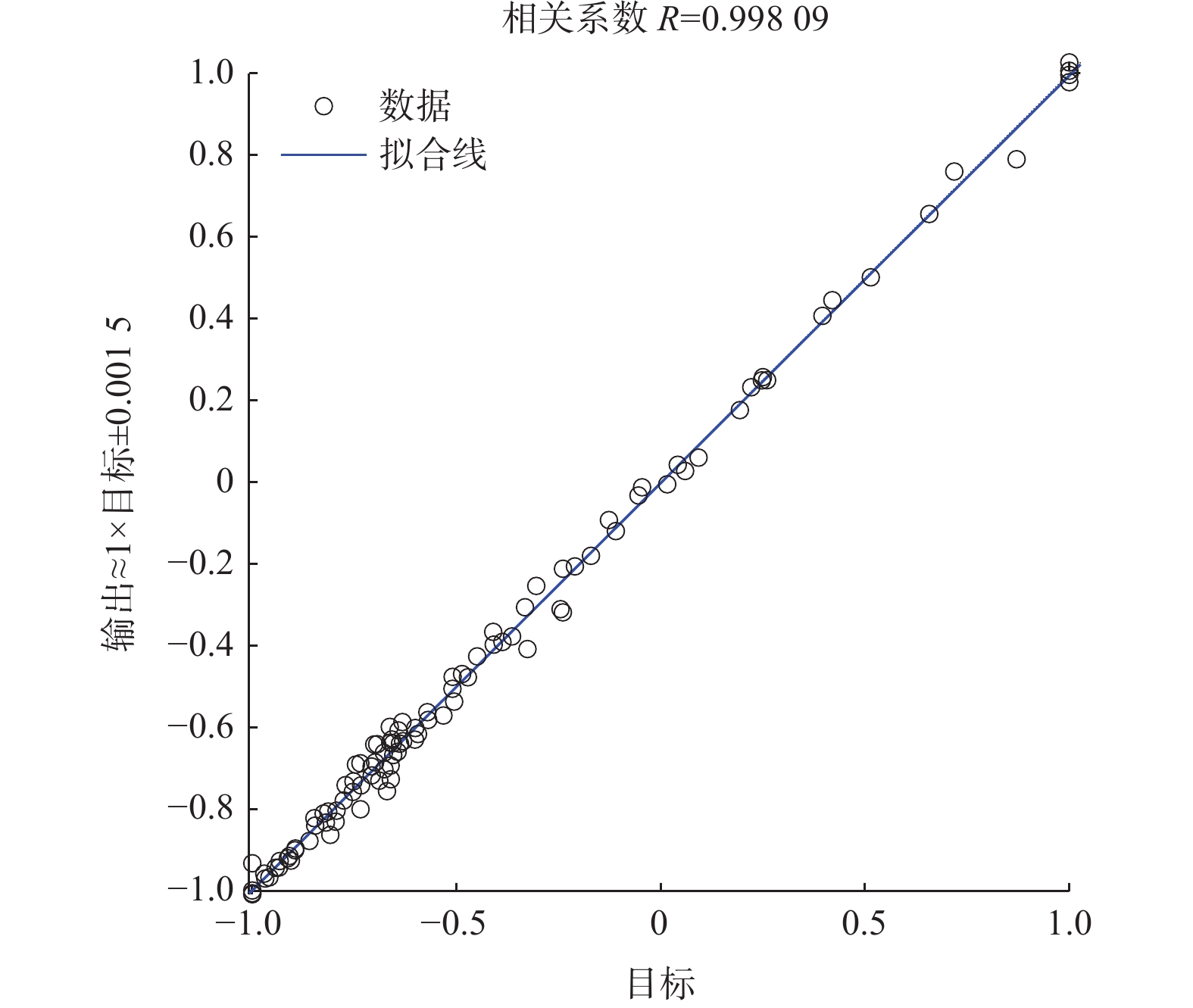
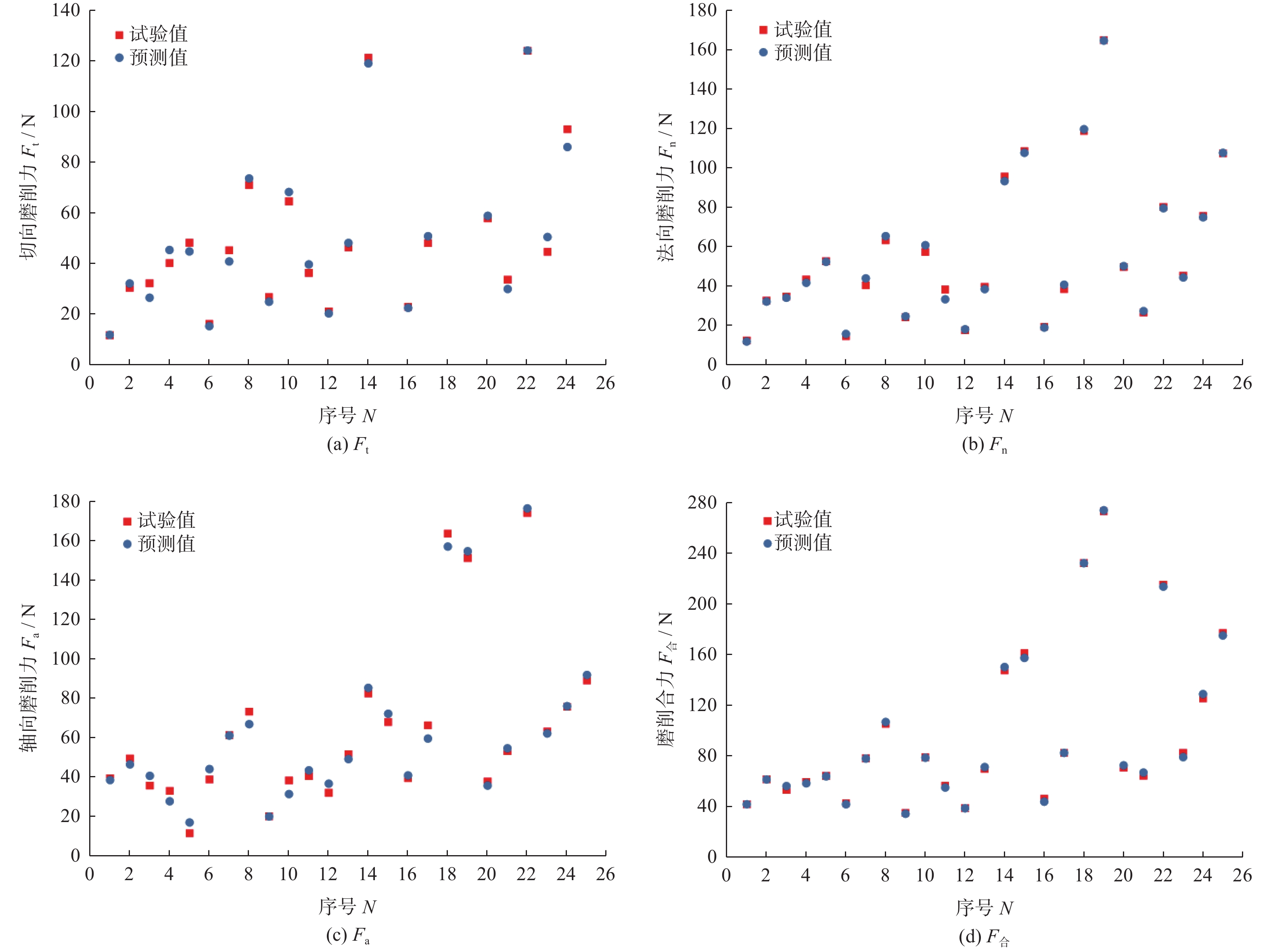
图5为BP神经网络训练样本的线性回归图。由图5可知,训练样本的相关系数R为0.998 09。图6为磨削力的预测值与试验值对比图,切向磨削力、法向磨削力、轴向磨削力和磨削合力的预测值相对试验值的平均相对误差分别为5.51%、3.10%、7.84%和1.75%,符合预测需求[20]。
为验证训练完成的神经网络的预测精度和稳定性,选取额外2组工艺参数,其预测值和试验值比较如表3所示,表中的相对误差是预测值相对试验值的结果。由表3可知:相对误差在−12.50%~5.28%,因此建立的神经网络模型具有较好的预测精度和稳定性。
表 3 神经网络预测值和试验值比较Table 3. Comparison between neural network predicted values and experimental values序号 A B C D 对比项目 Ft Fn Fa F合 1 6 2.5 7 000 2 500 试验值 / N 238.24 166.19 198.10 351.60 预测值 / N 235.03 163.42 177.17 325.18 相对误差 / % −1.35 −1.67 −10.57 −7.51 2 6 1.5 8 000 2 500 试验值 / N 83.22 48.48 83.11 127.21 预测值 / N 72.82 45.99 87.50 116.10 相对误差 / % −12.50 −5.14 5.28 −8.73 2.5 机器人磨削工艺参数优化
磨削工艺参数直接影响磨削力和加工效率,因此,将径向切深ae、轴向切深ap、主轴转速n、进给速度vw作为优化变量,以材料去除率RMRR为目标优化函数,约束条件由加工系统的实际情况确定。文中的主要约束条件包括:(1)磨削合力不超过机器人的最大负载;(2)主轴转速n不低于主轴最低转速,不高于最高转速;(3)进给速度vw不低于机器人最低运行速度,不高于最高运行速度;(4)径向切深ae不超过工具半径;(5)轴向切深ap不超过工具切削刃长度。即约束条件为:
$$ \left\{\begin{array}{l} F_合 \leqslant F_{\mathrm{r} \text{\_load}} \\ n_{\min } \leqslant n \leqslant n_{\max } \\ v_{\mathrm{w}_{\min }} \leqslant v_{\mathrm{w}} \leqslant v_{\mathrm{w}_{\max }} \\ a_{\mathrm{e}} \leqslant \dfrac{d}{2} \\ a_{\mathrm{p}} \leqslant l \end{array}\right.$$ (6) 式中:Fr_load为机器人的额定负载,其值为600 N;nmin、nmax为主轴最低、最高转速;$ {v_{\mathrm{w}}}_{_{\min}} $、$ {v_{{{\mathrm{w}}_{\max}}}} $为机器人最低及最高运行速度;l为工具切削刃长度。
遗传算法能够为求解复杂非线性问题提供一种全局寻优搜索方法[21]。将BP神经网络建立的磨削力预测模型作为功能函数,以材料去除率RMRR的倒数为目标优化函数,采用MATLAB进行遗传算法设计。设计时种群大小设置为100,遗传代数为200代,交叉概率为0.8,变异概率为0.2。通过遗传算法得到优化的工艺参数组合是径向切深ae = 2.28 mm,轴向切深ap = 2.98 mm,主轴转速n = 9 586.65 r/min,进给速度vw = 2 207.67 mm/min,此时的材料去除率预测值根据式(2)计算得到RMRRP = 14 999.79 mm3/min。同时,在此优化工艺参数下,材料去除率的试验值RMRRT = 14 194.44 mm3/min,试验值相对预测值的相对误差为−5.37%。
基于BP神经网络和遗传算法得到了机器人加工砂岩的磨削力预测结果和优化的磨削工艺参数组合,模型预测结果和试验结果有较高的一致性(表3)。但在实际生产加工中,还应考虑机器人加工系统刚度较低受力变形导致的实际材料去除率偏低、工具磨损和设备磨损加剧、能耗增加、噪声过大等情况。
3. 结论
采用正交试验方法,基于BP神经网络和遗传算法进行了机器人加工砂岩的磨削力预测和工艺参数优化,得出如下结论:
(1)磨削工艺参数轴向切深ap、径向切深ae、进给速度vw和主轴转速n对切向、法向、轴向磨削力分量和磨削合力的影响主次顺序不同,对切向磨削力影响的主次顺序为ap > ae > vw > n,对法向磨削力影响的主次顺序为ap > vw > ae > n,对轴向磨削力影响的主次顺序为n > ae > vw > ap,对磨削合力影响的主次顺序为vw > ae > vw > ap。4个磨削力基本上都随ae、ap、vw的增加呈增长趋势,随n的增加呈下降趋势。
(2)随着ae增加,法向和切向磨削力比呈下降趋势;随着ap增加,磨削力比在一定范围内波动;随着n增加,磨削力比呈先上升、后下降、再小幅上升趋势;随着vw增加,磨削力比呈先下降、后上升趋势。
(3)用正交试验数据进行BP神经网络训练并进行预测,切向、法向及轴向磨削力的预测值与试验值对比,轴向磨削力相对误差绝对值的平均值最大为7.84%,建立的神经网络模型具有较好的预测精度和稳定性,符合预测要求。
(4)采用遗传算法,以材料去除率RMRR的倒数为目标优化函数,得到优化的工艺参数组合为径向切深ae = 2.28 mm,轴向切深ap = 2.98 mm,主轴转速n = 9 586.65 r/min,进给速度vw = 2 207.67 mm/min,此时的材料去除率预测值RMRRP = 14 999.79 mm3/min。同时,在此优化参数下,材料去除率的试验值RMRRT = 14 194.44 mm3/min,试验值相对预测值的相对误差为−5.37%。
-
表 1 磨削力的正交试验因素及水平
Table 1. Orthogonal test factors and levels of grinding force
水平 因素 径向切深
ae / mm
A轴向切深
ap / mm
B主轴转速
n / (r·min−1)
C进给速度
vw / ( mm·min−1)
D1 2 1.0 5 000 500 2 3 1.5 6 000 1 000 3 4 2.0 7 000 1 500 4 5 2.5 8 000 2 000 5 6 3.0 9 000 2 500 表 2 磨削力正交试验数据及极差分析结果
Table 2. Orthogonal experimental data and range analysis results of grinding forces
序号 A B C D 切向磨削力
Ft / N法向磨削力
Fn / N轴向磨削力
Fa / N磨削合力
F合 / N法向和切向
磨削力比Kf材料去除率
RMRR / (mm3·min−1)1 2 1.0 5 000 500 12.10 12.59 39.83 41.93 1.04 1.00 × 103 2 2 1.5 6 000 1 000 30.89 32.94 49.82 61.79 1.07 3.00 × 103 3 2 2.0 7 000 1 500 32.65 34.93 36.05 53.23 1.07 6.00 × 103 4 2 2.5 8 000 2 000 40.57 43.59 33.32 59.70 1.07 10.00 × 103 5 2 3.0 9 000 2 500 48.55 52.92 11.78 64.44 1.09 15.00 × 103 6 3 1.0 6 000 1 500 16.59 14.83 39.14 42.89 0.89 4.50 × 103 7 3 1.5 7 000 2 000 45.56 40.67 61.57 78.22 0.89 9.00 × 103 8 3 2.0 8 000 2 500 71.34 63.60 73.6 105.57 0.89 15.00 × 103 9 3 2.5 9 000 500 27.15 24.36 20.38 35.11 0.90 3.75 × 103 10 3 3.0 5 000 1 000 64.88 57.65 38.59 79.14 0.89 9.00 × 103 11 4 1.0 7 000 2 500 36.68 38.50 40.87 56.59 1.05 10.00 × 103 12 4 1.5 8 000 500 21.46 17.72 32.41 38.90 0.83 3.00 × 103 13 4 2.0 9 000 1 000 46.78 39.78 51.96 69.92 0.85 8.00 × 103 14 4 2.5 5 000 1 500 121.43 96.06 82.76 147.82 0.79 15.00 × 103 15 4 3.0 6 000 2 000 143.56 108.88 68.30 161.44 0.76 24.00 × 103 16 5 1.0 8 000 1 000 23.37 19.53 39.76 46.38 0.84 5.00 × 103 17 5 1.5 9 000 1 500 48.45 38.67 66.55 82.67 0.80 11.25 × 103 18 5 2.0 5 000 2 000 164.93 119.23 163.9 232.69 0.72 20.00 × 103 19 5 2.5 6 000 2 500 227.37 165.41 151.50 273.57 0.73 31.25 × 103 20 5 3.0 7 000 500 58.23 50.03 38.07 70.97 0.86 7.50 × 103 21 6 1.0 9 000 2 000 34.05 26.80 53.53 64.63 0.79 12.00 × 103 22 6 1.5 5 000 2 500 124.19 80.59 174.40 215.62 0.65 22.50 × 103 23 6 2.0 6 000 500 45.00 45.49 63.48 82.59 1.01 6.00 × 103 24 6 2.5 7 000 1 000 93.31 75.93 75.99 125.78 0.81 15.00 × 103 25 6 3.0 8 000 1 500 146.63 107.90 89.36 177.41 0.74 27.00 × 103 切向
磨削力
Ft / NKi1 32.95 24.56 97.51 32.79 ap > ae > vw > n Ki2 45.10 54.11 92.68 51.84 Ki3 73.98 72.14 53.28 73.15 Ki4 104.47 101.97 60.68 85.73 Ki5 88.64 92.37 41.00 101.63 Ri 71.52 77.41 56.51 68.84 法向
磨削力
Fn / NKi1 35.40 22.45 73.22 30.04 ap > vw > ae > n Ki2 40.22 42.12 73.51 45.17 Ki3 60.19 60.61 48.01 58.48 Ki4 78.58 81.07 50.47 67.83 Ki5 67.34 75.48 36.51 80.20 Ri 43.18 58.62 37.00 50.17 轴向
磨削力
Fa / NKi1 34.16 42.63 99.90 38.83 n > ae > vw > ap Ki2 46.66 76.95 74.45 51.22 Ki3 55.26 77.80 50.51 62.77 Ki4 91.96 72.79 53.69 76.12 Ki5 91.35 49.22 40.84 90.43 Ri 57.80 35.17 59.06 51.60 磨削
合力
F合 / NKi1 56.22 50.48 143.44 53.90 vw > ae > n > ap Ki2 68.18 95.44 124.46 76.60 Ki3 94.93 108.80 76.96 100.80 Ki4 141.26 128.40 85.59 119.33 Ki5 133.21 110.68 63.35 143.16 Ri 85.04 77.91 80.09 89.26 法向和
切向磨
削力比
KfKi1 1.068 0.922 0.819 0.927 ae > n > vw > ap Ki2 0.893 0.846 0.892 0.891 Ki3 0.855 0.909 0.937 0.858 Ki4 0.789 0.861 0.873 0.847 Ki5 0.799 0.866 0.885 0.882 Ri 0.280 0.075 0.119 0.080 表 3 神经网络预测值和试验值比较
Table 3. Comparison between neural network predicted values and experimental values
序号 A B C D 对比项目 Ft Fn Fa F合 1 6 2.5 7 000 2 500 试验值 / N 238.24 166.19 198.10 351.60 预测值 / N 235.03 163.42 177.17 325.18 相对误差 / % −1.35 −1.67 −10.57 −7.51 2 6 1.5 8 000 2 500 试验值 / N 83.22 48.48 83.11 127.21 预测值 / N 72.82 45.99 87.50 116.10 相对误差 / % −12.50 −5.14 5.28 −8.73 -
[1] 张永长, 杨涛, 纪静, 等. 厦门市翔安区2017年石材加工行业职业卫生现状调查 [J]. 职业卫生与应急救援,2018,36(4):328-330,353. doi: 10.16369/j.oher.issn.1007-1326.2018.04.013ZHANG Yongchang, YANG Tao, JI Jing, et al. Investigation on occupational health work of stone industries in Xiang’an District of Xiamen City in 2017 [J]. Occup Health and Emergency Rescue,2018,36(4):328-330,353. doi: 10.16369/j.oher.issn.1007-1326.2018.04.013 [2] 曾晓立, 李英娥, 林立, 等. 某厂石雕作业工人生活质量调查 [J]. 中国工业医学杂志,2018,31(2):135-137. doi: 10.13631/j.cnki.zggyyx.2018.02.023ZENG Xiaoli, LI Yinge, LIN Li, et al. Survey on life quality of stone carving workers [J]. Chinese Journal of Industrial Medicine,2018,31(2):135-137. doi: 10.13631/j.cnki.zggyyx.2018.02.023 [3] NGUYEN T M, SURDILOVIC D, KRUGER J, et al. Efficient application of industrial robots for automated stone sculptures milling: 1st international conference on stone and concrete machining [C]// Hannover: Institute of Production Engineering and Machine Tool, 2011. [4] 黄吉祥, 尹方辰, 黄身桂, 等. 机器人石材雕刻粗加工能耗建模与优化分析 [J]. 华侨大学学报(自然科学版),2024,45(4):471-477. doi: 10.11830/ISSN.1000-5013.202311024HUANG Jixiang, YIN Fangchen, HUANG Shengui, et al. Modeling and optimization analysis of energy consumption in rough machining of robotic stone carving [J]. Journal of Huaqiao University (Natural Science),2024,45(4):471-477. doi: 10.11830/ISSN.1000-5013.202311024 [5] 周进. 基于时间尺度函数的工业机器人加工系统节能优化方法与典型应用研究 [D]. 重庆: 重庆大学, 2022.ZHOU Jin. Time-scaling-based energy-saving optimization method and typical application study of robot machining system [D]. Chongqing: Chongqing University, 2022. [6] 籍永建, 姚利诚. 机器人铣削加工颤振自适应识别方法研究 [J]. 中国机械工程,2023,34(18):2165-2176. doi: 10.3969/j.issn.1004-132X.2023.18.003JI Yongjian, YAO Licheng. Research on self-adaptive chatter recognition method for robotic milling [J]. China Mechanical Engineering,2023,34(18):2165-2176. doi: 10.3969/j.issn.1004-132X.2023.18.003 [7] LI J, LI B, SHEN N, et al. Effect of the cutter path and the workpiece clamping position on the stability of the robotic milling system [J]. International Journal of Advanced Manufacturing Technology,2017,89(9/10/11/12):2919-2933. doi: 10.1007/s00170-016-9759-x [8] 陈齐志. 工业机器人铣削系统颤振分析与加工精度提升方法研究 [D]. 济南: 山东大学, 2022.CHEN Qizhi. Research on chatter analysis and machining accuracy improvement method of industrial robotic milling system [D]. Jinan: Shandong University, 2022. [9] 巩亚东, 赵显力, 张伟健, 等. 机器人砂带磨削单磨粒材料去除影响因素 [J]. 东北大学学报(自然科学版),2023,44(9):1285-1291. doi: 10.12068/j.issn.1005-3026.2023.09.009GONG Yadong, ZHAO Xianli, ZHANG Weijian, et al. Factors influencing single abrasive material removal for robotic abrasive belt grinding [J]. Journal of Northeastern University ( Natural Science),2023,44(9):1285-1291. doi: 10.12068/j.issn.1005-3026.2023.09.009 [10] 陈庚, 向华, 叶寒, 等. 考虑法向接触力变化的机器人砂带磨削参数研究 [J]. 中国机械工程,2023,34(7):803-811,820. doi: 10.3969/j.issn.1004-132X.2023.07.006CHEN Geng, XIANG Hua, YE Han, et al. Research on robot abrasive belt grinding parameters considering the change of normal contact force [J]. China Mechanical Engineering,2023,34(7):803-811,820. doi: 10.3969/j.issn.1004-132X.2023.07.006 [11] 李东阳, 谢海龙, 王清辉, 等. 基于力反馈的机器人砂带磨削虚拟示教轨迹规划方法 [J]. 现代制造工程,2022,(5):30-35. doi: 10.16731/j.cnki.1671-3133.2022.05.005LI Dongyang, XIE Hailong, WANG Qinghui, et al. Haptic feedback based virtual teaching method of toolpath planning for robot belt grinding processes [J]. Modern Manufacturing Engineering,2022,(5):30-35. doi: 10.16731/j.cnki.1671-3133.2022.05.005 [12] 李弘毅, 阮玉镇, 汤绍钊, 等. 机器人磨削工艺参数对系统固有频率影响的试验研究 [J]. 机床与液压,2022,50(3):49-53. doi: 10.3969/j.issn.1001-3881.2022.03.009LI Hongyi, RUAN Yuzhen, TANG Shaozhao, et al. Experimental study on the influence of robot grinding parameters on system natural frequency [J]. Machine Tool & Hydraulics,2022,50(3):49-53. doi: 10.3969/j.issn.1001-3881.2022.03.009 [13] 杨平, 杨冰雅, 肖硕男. 合模线飞边在线测量与机器人智能磨抛加工技术 [J]. 制造业自动化,2024,46(2):129-135. doi: 10.3969/j.issn.1009-0134.2024.02.026YANG Ping, YANG Bingya, XIAO Shuonan. On-line measurement and intelligent grinding processing technology by using robots for joint fin [J]. Manufacturing Automation,2024,46(2):129-135. doi: 10.3969/j.issn.1009-0134.2024.02.026 [14] 王超, 郑乾健, 肖聚亮, 等. 考虑时变磨损的机器人磨抛参数优化研究 [J]. 天津大学学报(自然科学与工程技术版),2023,56(2):127-136. doi: 10.11784/tdxbz202110006WANG Chao, ZHENG Qianjian, XIAO Juliang, et al. Research on optimization of robot grinding and polishing parameters considering time-varying wear [J]. Journal of Tianjin University (Science and Technology),2023,56(2):127-136. doi: 10.11784/tdxbz202110006 [15] 田凤杰, 车长林, 李孝辉, 等. 机器人磨抛微量去除飞机蒙皮包铝工艺试验 [J]. 航空制造技术,2022,65(13):56-62. doi: 10.16080/j.issn1671-833x.2022.13.056TIAN Fengjie, CHE Changlin, LI Xiaohui, et al. Experiment on micro-removal for aluminum clad of aircraft skin by robotic grinding [J]. Aeronautical Manufacturing Technology,2022,65(13):56-62. doi: 10.16080/j.issn1671-833x.2022.13.056 [16] 黄吉祥, 刘舒颖, 黄辉, 等. 机械臂加工花岗岩的力和工具磨损特性 [J]. 华侨大学学报(自然科学版),2018,39(2):159-165. doi: 10.11830/ISSN.1000-5013.201712065HUANG Jixiang, LIU Shuying, HUANG Hui, et al. Forces and tool wear characteristics in granite grinding by robotic [J]. Journal of Huaqiao University (Natural Science),2018,39(2):159-165. doi: 10.11830/ISSN.1000-5013.201712065 [17] 武沙桐. 磨削力约束下的立体石雕机器人加工轨迹规划研究 [D]. 厦门: 华侨大学, 2022.WU Shatong. Research on robot trajectory planning of three-dimensional stone carving based on grinding force constraint [D]. Xiamen: Huaqiao University, 2022. [18] 王雷. 基于BP神经网络的钛合金加工切削力预测模型研究 [D]. 天津: 天津理工大学, 2016.WANG Lei. Research on the cutting force prediction model of titanium alloy with BP neural network [D]. Tianjin: Tianjin University of Technology, 2016. [19] 刘寿军, 肖开永, 牛腾, 等. 基于神经网络-遗传算法的泵体零件热锻模具磨损与应力分析 [J]. 锻压技术,2024,49(2):208-214. doi: 10.13330/j.issn.1000-3940.2024.02.026LIU Shoujun, XIAO Kaiyong, NIU Teng, et al. Analysis on wear and stress of hot forging die for pump body parts based on neural network-genetic algorithm [J]. Forging & Stamping Technology,2024,49(2):208-214. doi: 10.13330/j.issn.1000-3940.2024.02.026 [20] 王晶. 基于神经网络的机器人加工花岗石多目标工艺优化 [D]. 厦门: 华侨大学, 2020.WANG Jing. Multi-objective process parameters optimization of granite robot machining based on neural network [D]. Xiamen: Huaqiao University, 2020. [21] 梁强, 张贤明, 杜彦斌, 等. 基于灰色关联分析的齿环热精锻成形工艺参数优化 [J]. 计算机集成制造系统,2022,28(4):1020-1029. doi: 10.13196/j.cims.2022.04.006LIANG Qiang, ZHANG Xianming, DU Yanbin, et al. Parameters optimization in hot precision forging process of synchronizer ring based on grey relational analysis [J]. Computer Integrated Manufacturing Systems,2022,28(4):1020-1029. doi: 10.13196/j.cims.2022.04.006 -





 下载:
下载:






 下载:
下载:







 邮件订阅
邮件订阅 RSS
RSS
