基于当量磨削层厚度的整体刀具容屑槽磨削功率模型

任磊; 潘江涛; 向道辉; 马俊金; 崔晓斌

doi:10.13394/j.cnki.jgszz.2024.0003

基于当量磨削层厚度的整体刀具容屑槽磨削功率模型

doi: 10.13394/j.cnki.jgszz.2024.0003

河南理工大学机械与动力工程学院, 河南焦作 454003

基金项目: 国家自然科学基金青年项目（52005165）；河南省科技攻关项目（242102221016）。

详细信息

作者简介:
通信作者：任磊，男，1991年生，博士、讲师。主要研究方向：高性能复杂刀具精密加工技术。E-mail：renlei@hpu.edu.cn

中图分类号: TG71; TG74; TG58; TG593
计量
- 文章访问数: 55
- HTML全文浏览量: 28
- PDF下载量: 3
- 被引次数: 0
出版历程
- 收稿日期: 2024-01-04
- 修回日期: 2024-03-04
- 录用日期: 2024-03-13
- 网络出版日期: 2025-03-24
- 刊出日期: 2025-02-20

Grinding power model for flute grinding of solid tools based on equivalent chip thickness

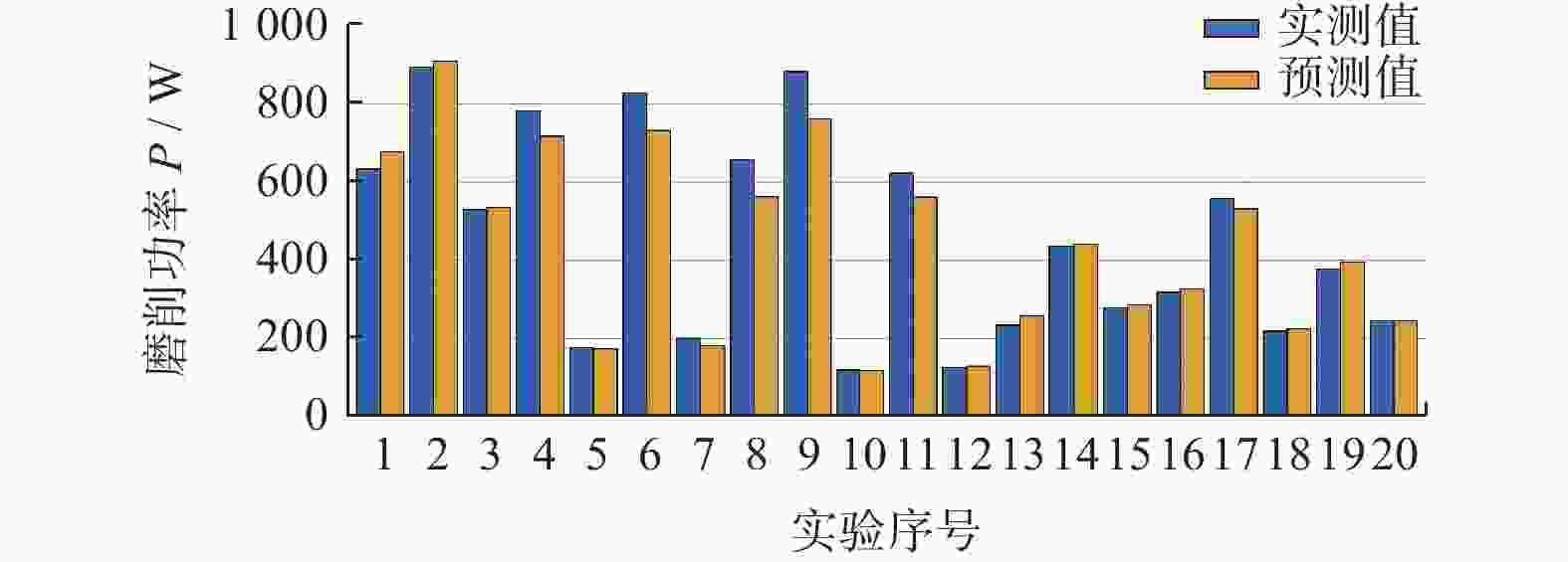
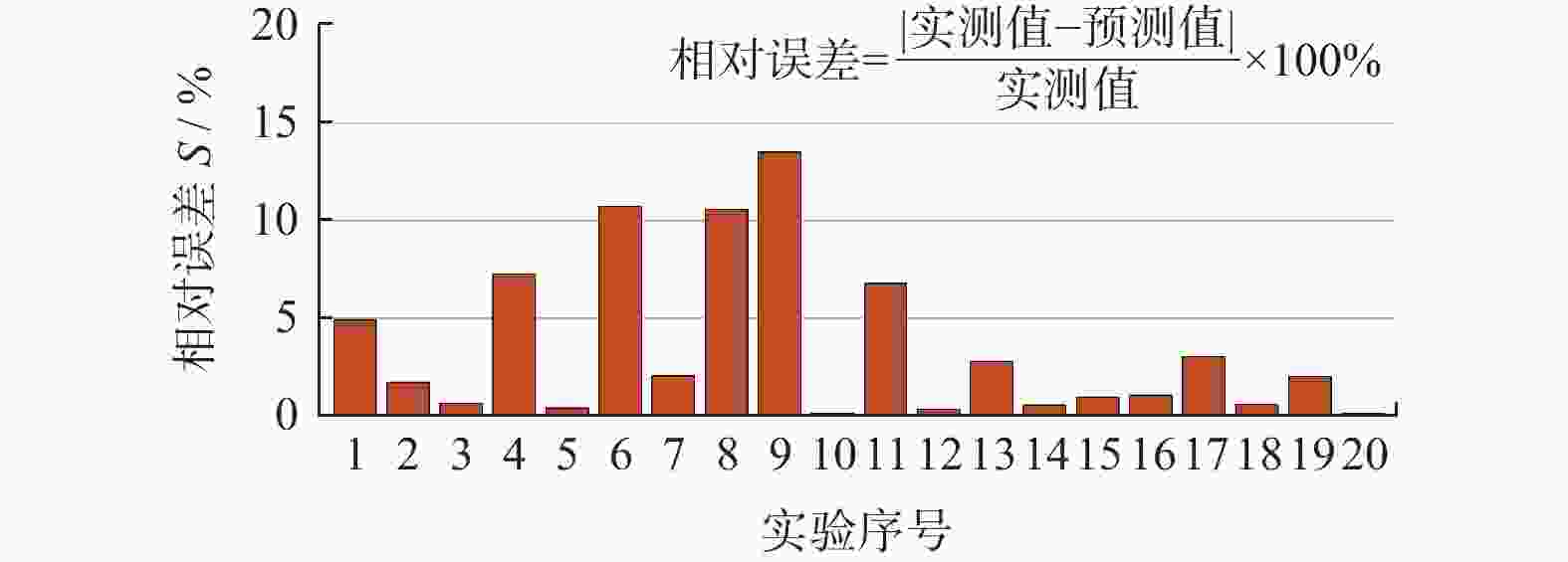
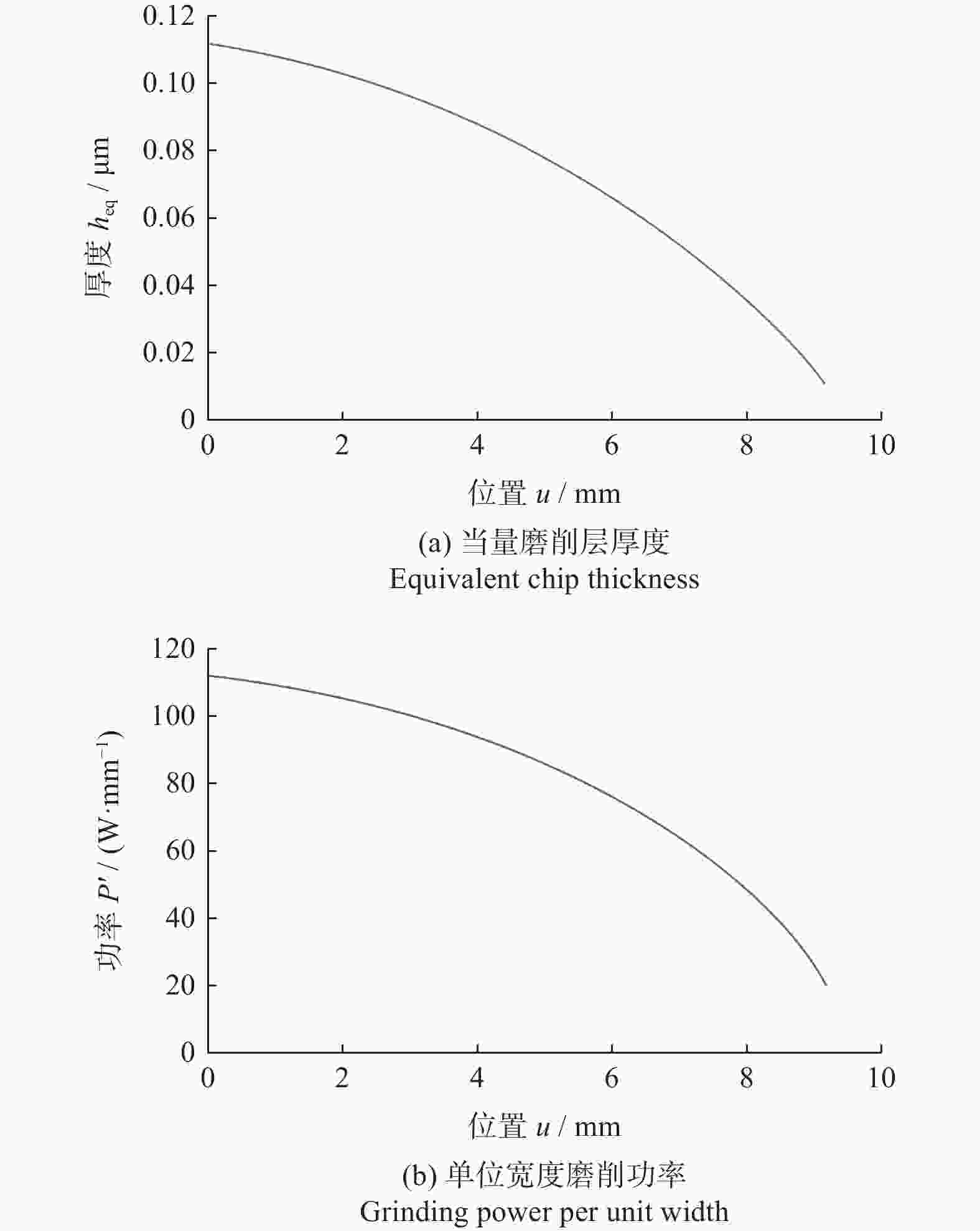
School of Mechanical and Power Engineering, Henan Polytechnic University, Jiaozuo 454003, Henan, China

摘要

摘要: 磨削功率与整体刀具容屑槽的磨削质量密切相关。提出一种基于当量磨削层厚度的整体刀具容屑槽磨削功率模型，将砂轮离散化为一组等厚度的砂轮薄片，由砂轮与刀具间的瞬时接触线计算各砂轮薄片的接触弧长；再通过引入磨削接触区形状系数计算沿砂轮宽度方向逐渐变化的当量磨削深度和当量进给速度，得到各砂轮薄片对应的当量磨削层厚度；在此基础上建立容屑槽磨削功率模型，并通过磨削实验对模型进行验证。结果表明：模型的功率预测值与测量值间的最大相对误差 < 15.0%；沿砂轮宽度方向的最大当量磨削层厚度和最大单位宽度磨削功率存在于砂轮边缘处，将导致砂轮宽度方向上的非均匀磨损。
- 整体刀具 /
- 容屑槽 /
- 磨削功率 /
- 当量磨削层厚度 /
- 螺旋槽
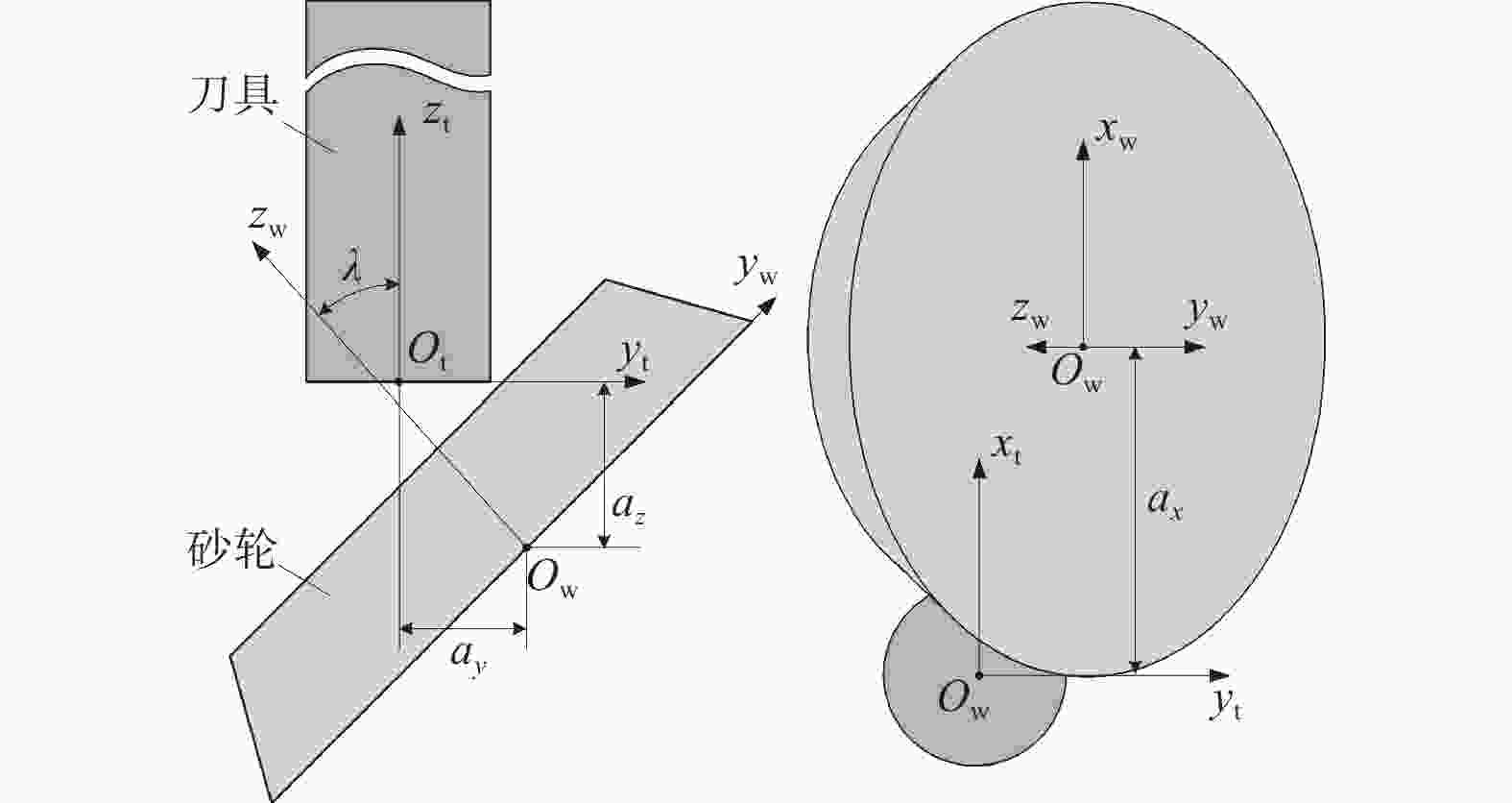
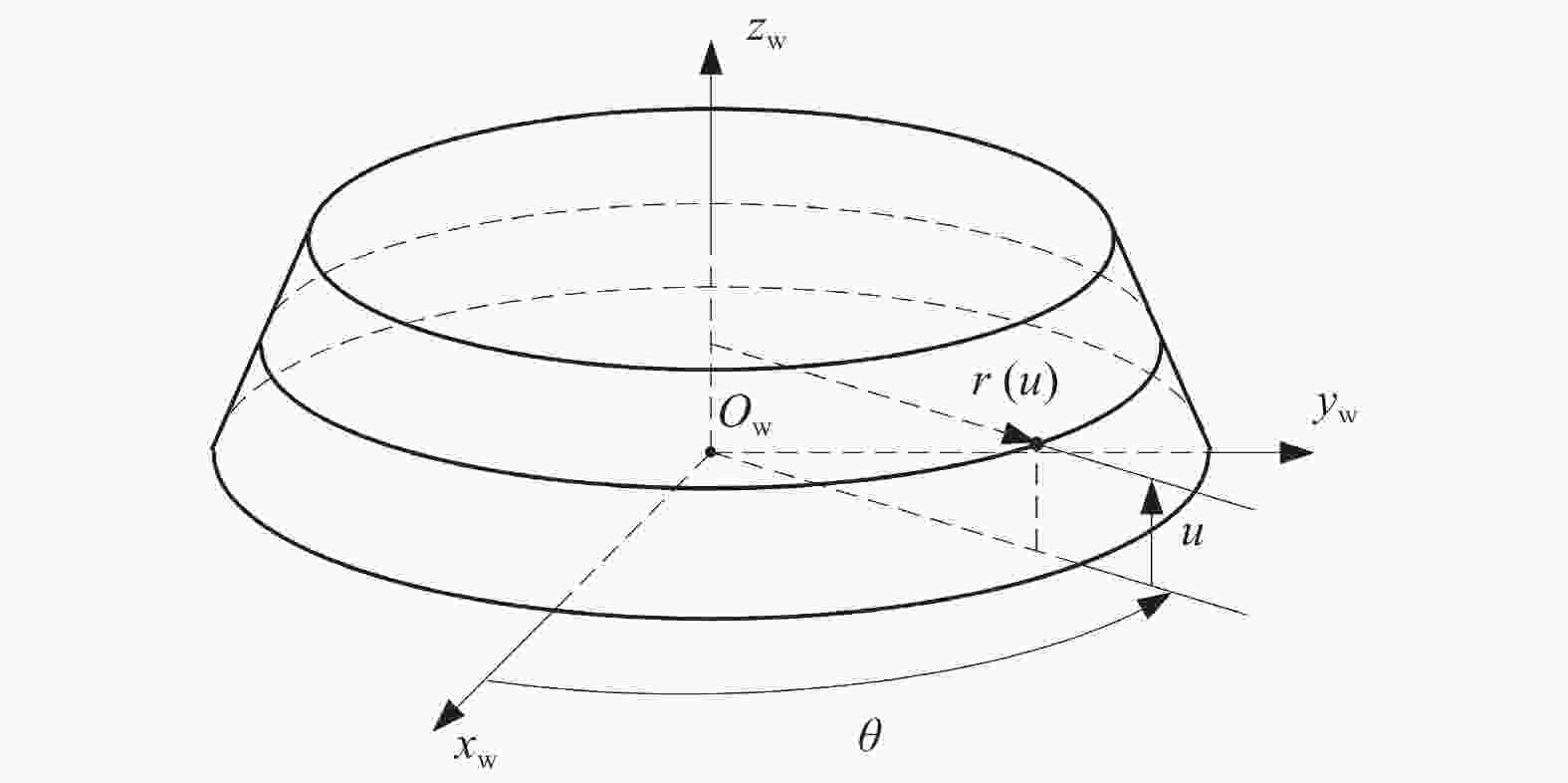
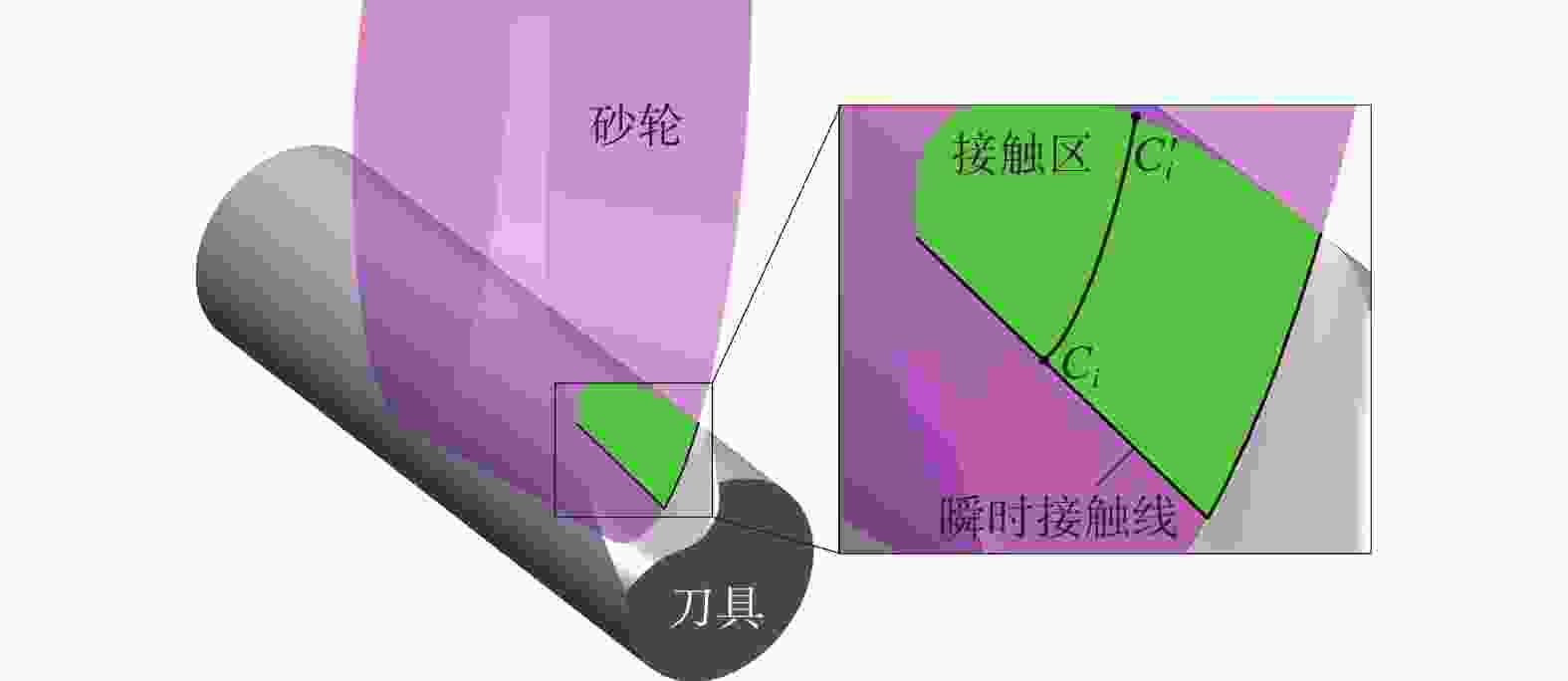
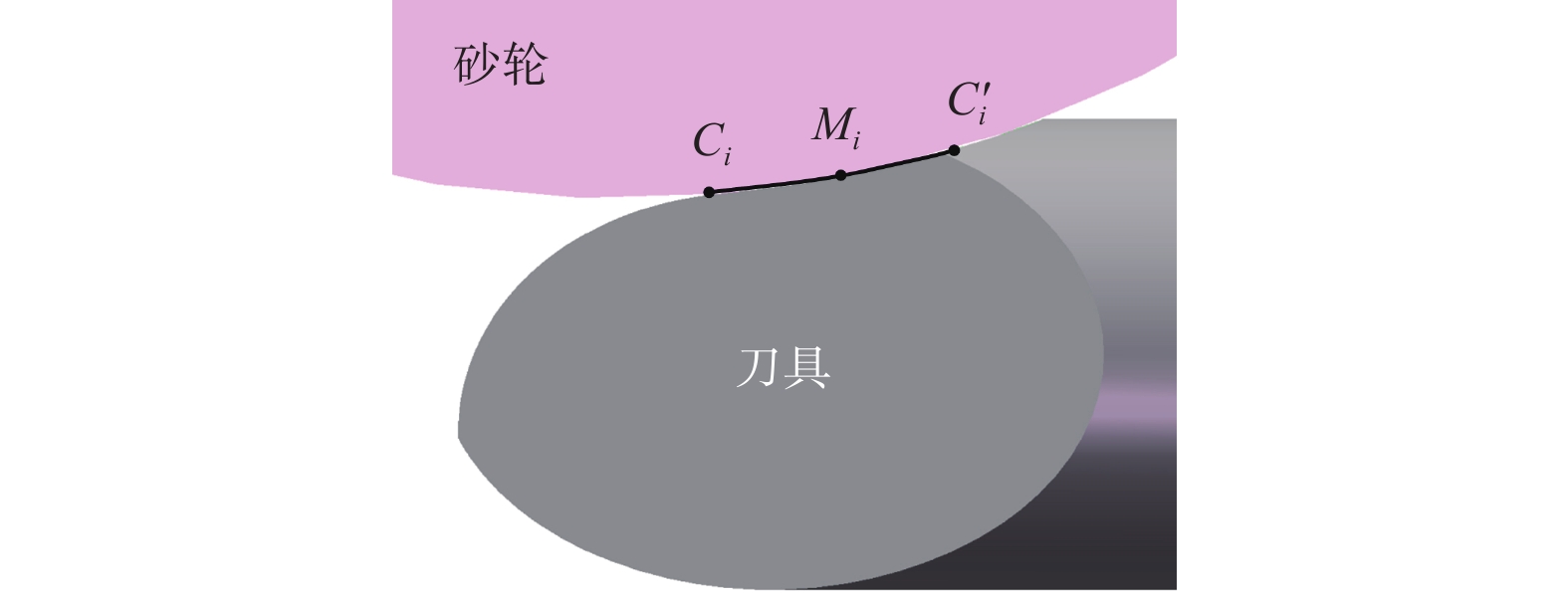
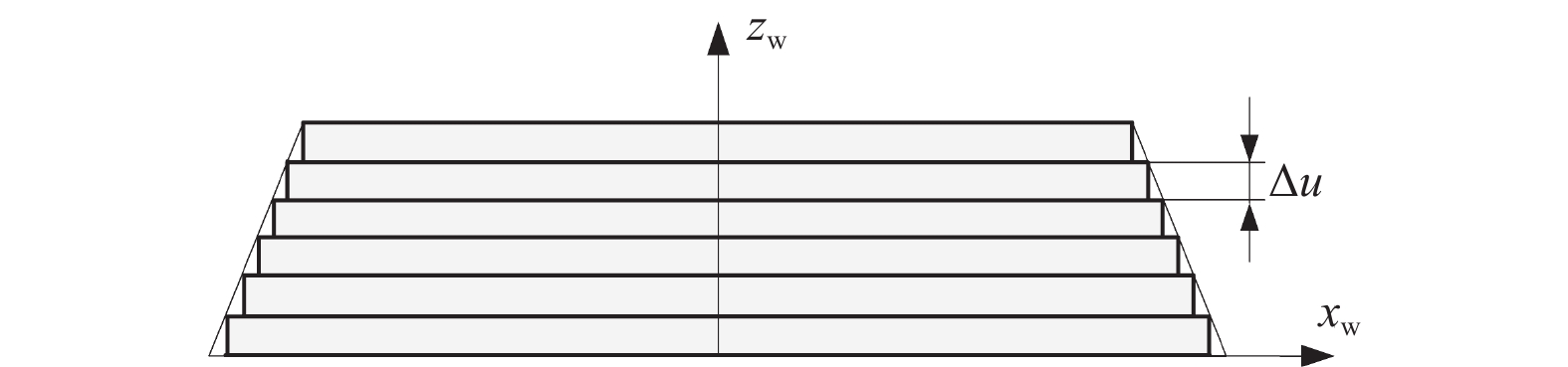
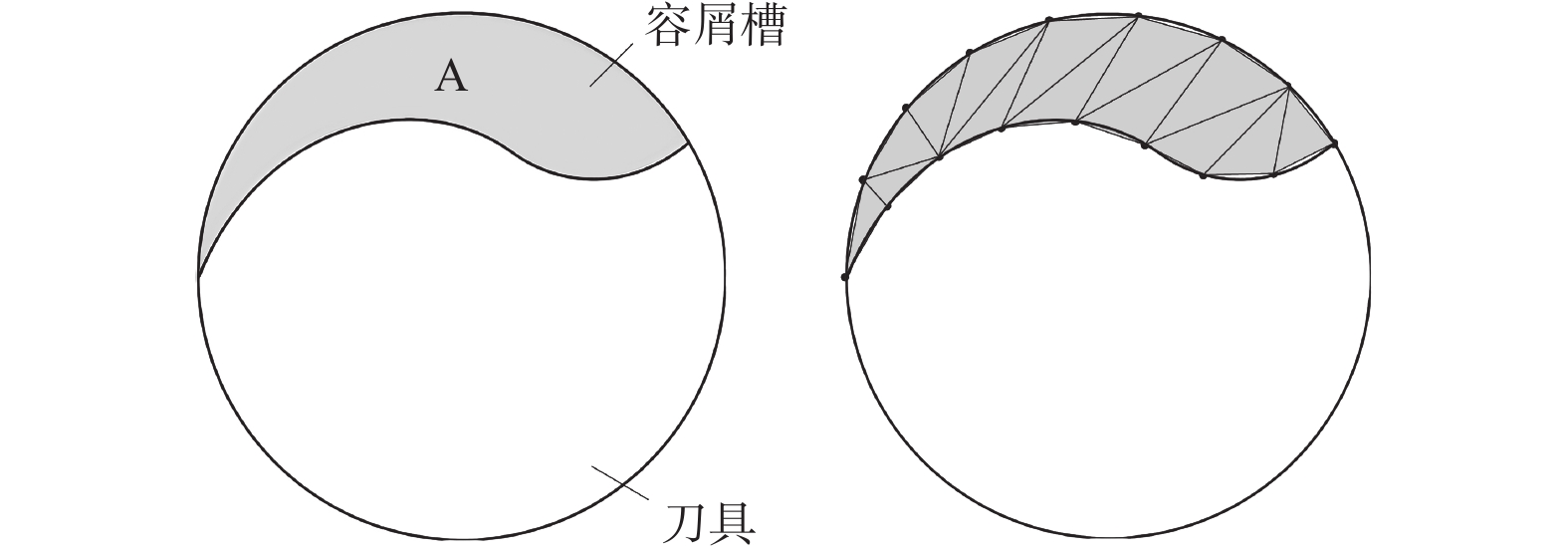
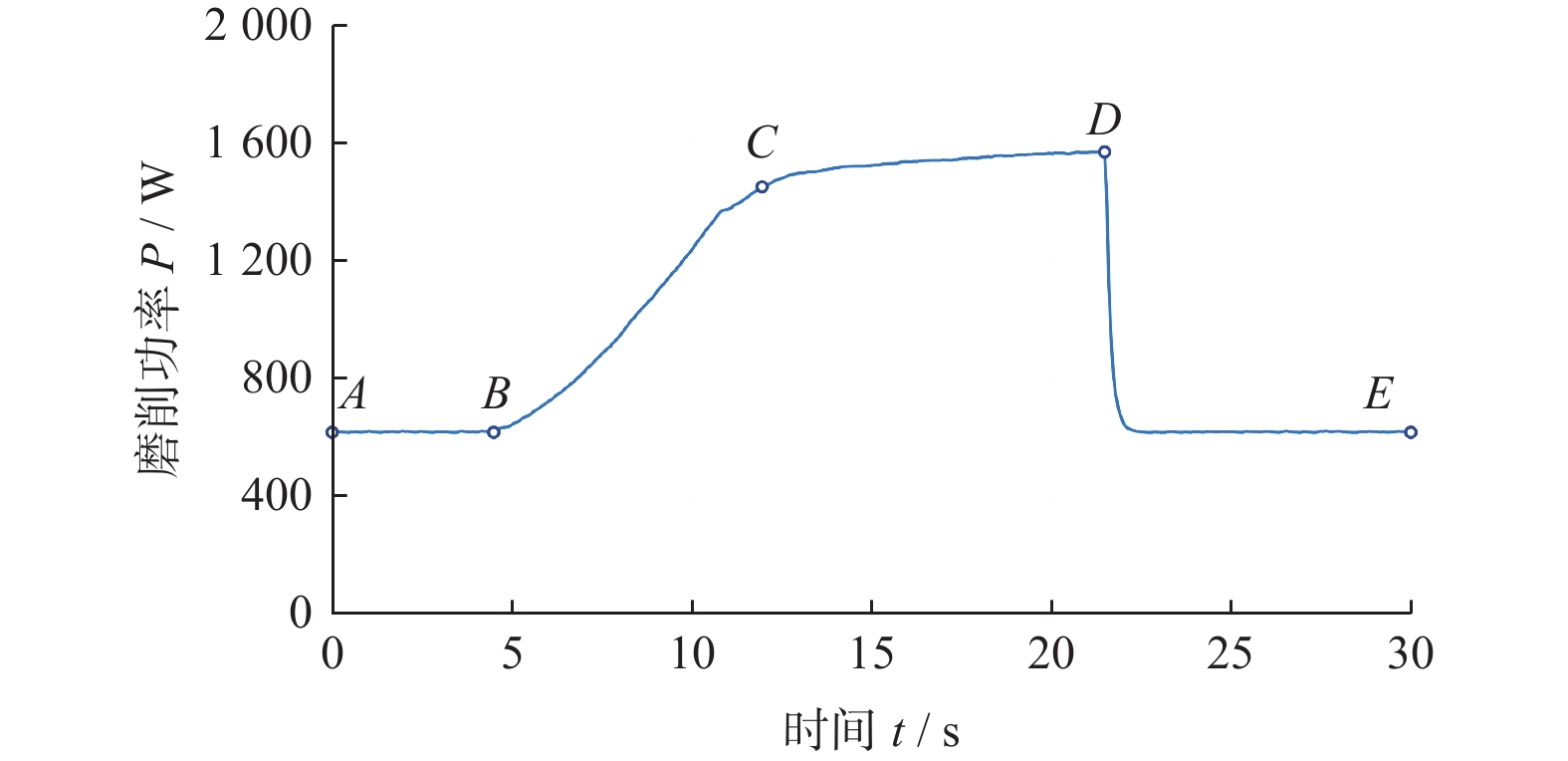
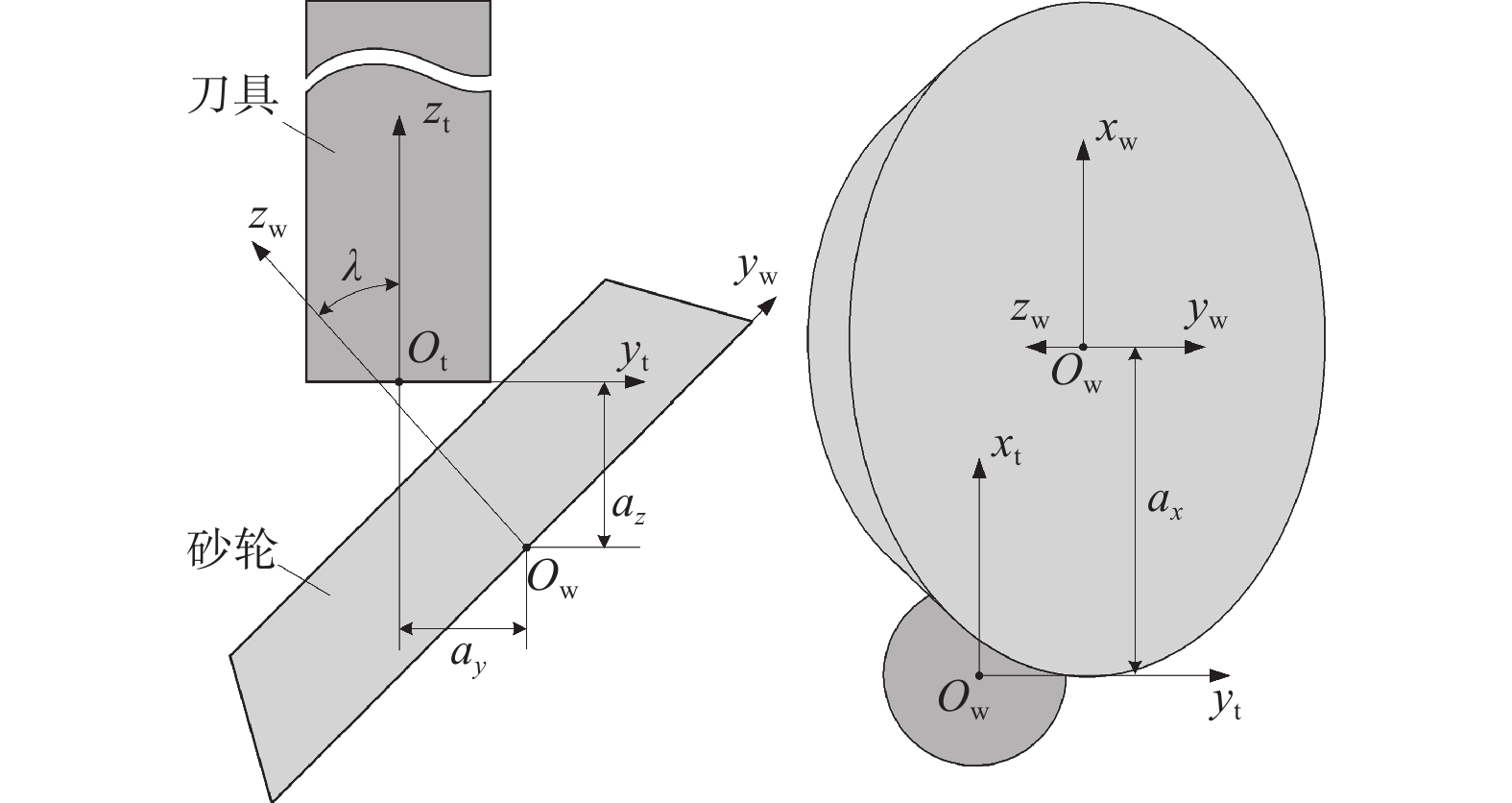
Abstract: Objectives During the flute grinding process of solid tools, the majority of grinding power is converted into grinding heat. Excessive grinding power can cause a rapid temperature rise on the surface of the contact area between the grinding wheel and the tool, which can easily lead to grinding burns and eventually tool failure. A grinding power model for flute grinding of solid tools is proposed based on equivalent chip thickness, aiming to achieve precise prediction and control of grinding power for flute grinding. Methods A kinematic model for flute grinding is established using homogeneous coordinate transformation. On this basis, according to the theory of conjugate surfaces, the instantaneous contact line between the grinding wheel surface and the flute surface during the grinding process is obtained, and the grinding wheel is discretized into a set of equally thick grinding wheel slices. The grinding contact arc length is obtained by calculating the intersection points between the grinding wheel slices and the tool cylindrical surface. Flute grinding is regarded as external cylindrical grinding with a special contact zone shape. By introducing the contact-area-shape coefficient to define the equivalent grinding depth and the equivalent feed rate of each grinding wheel slice, the formula for calculating the equivalent grinding layer thickness of flute grinding is derived. When the linear speed of the grinding wheel, the axial feed speed of the workpiece, and the grinding contact arc length of each grinding wheel slice are known, the equivalent chip thickness of each grinding wheel slice can be calculated as long as the shape coefficient of the contact area is given. The cross-section profiles of the chute are discretized into small triangles, and the area of the cross-section profile of the chute is obtained by calculating the area of each triangle. The material removal rate of the chute during grinding is determined by combining the axial feed velocity of the workpiece. According to the principle of conservation of material removal rate, the formula for the shape coefficient of the contact area is derived. Based on the mathematical relationship between the local grinding power of each grinding wheel slice and the thickness of the equivalent grinding layer, the empirical model for flute grinding power is established. The experimental verification of the model is carried out on an ANCA MX7 CNC tool grinding machine. The flute with a spiral angle of 30° is ground on a cemented carbide rod with a metal-bonded diamond wheel. The spindle power data of the machine tool PLC is recorded using the data recording function of iGrind grinding software. The spindle power includes grinding power and spindle idle power, so grinding power is obtained by subtracting idle power from spindle power. Twenty sets of grinding experiments are carried out under different grinding parameters, and an overdetermined equation set is established by substituting the grinding power data of four sets of experiments into the power model. By solving this equation system, the two empirical constants in the model are obtained. Then, the grinding power model is used to predict the grinding powers of twenty sets of grinding experiments, and the predicted grinding powers are compared with the actual grinding powers. Results The comparison results show that the predicted grinding powers are close to the actual grinding powers, and the maximum relative error of the predicted grinding power is less than 15%. The equivalent chip thickness of each wheel slice and the grinding power per unit width vary gradually along the width of the grinding wheel, and the maximum equivalent chip thickness and the maximum grinding power per unit width exist at the edge of the grinding wheel. Conclusions The proposed grinding power model based on equivalent chip thickness can precisely predict the grinding power during the flute grinding process of solid tools, and obtain the distribution of grinding power in the width direction of the grinding wheel. The grinding power can be precisely controlled by adjusting grinding parameters with this model, and the maximum equivalent chip thickness and the maximum grinding power per unit width exist at the edge of the grinding wheel during the grinding process of the chute, which will lead to non-uniform wear in the direction of the width of the grinding wheel.
- solid tool /
- flute /
- grinding power /
- equivalent chip thickness /
- helical groove

HTML全文

图 1 砂轮相对刀具的初始位置

Figure 1. Initial position of grinding wheel relative to cutting tool

下载: 全尺寸图片幻灯片

图 2 砂轮回转面的几何定义

Figure 2. Geometric definition of surface of revolution of grinding wheel

下载: 全尺寸图片幻灯片

图 3 砂轮与容屑槽的瞬时接触线

Figure 3. Instantaneous contact line between grinding wheel and flute

下载: 全尺寸图片幻灯片

图 4 砂轮与刀具的接触弧

Figure 4. Arc of contact between grinding wheel and cutting tool

下载: 全尺寸图片幻灯片

图 5 砂轮离散化为一组砂轮薄片

Figure 5. Grinding wheel discretized into a set of wheel slices

下载: 全尺寸图片幻灯片

图 6 容屑槽的横截面廓形

Figure 6. Cross-sectional profile of flute

下载: 全尺寸图片幻灯片

图 7 ANCA MX7五轴数控工具磨床

Figure 7. ANCA MX7 five-axis CNC tool grinder

下载: 全尺寸图片幻灯片

图 8 实验用1A1砂轮的几何形状

Figure 8. Geometry of 1A1 grinding wheel used in experiments

下载: 全尺寸图片幻灯片

图 9 磨削功率变化曲线

Figure 9. Variation curve of grinding power

下载: 全尺寸图片幻灯片

图 10 各组实验的实测与预测磨削功率

Figure 10. Measured and predicted grinding power in each experiment

下载: 全尺寸图片幻灯片

图 11 各组实验预测磨削功率的相对误差

Figure 11. Relative error of predicted grinding power in each experiment

下载: 全尺寸图片幻灯片

图 12 砂轮宽度方向上的当量磨削层厚度和单位宽度磨削功率

Figure 12. Equivalent chip thickness and grinding power per unit width along grinding wheel width

下载: 全尺寸图片幻灯片

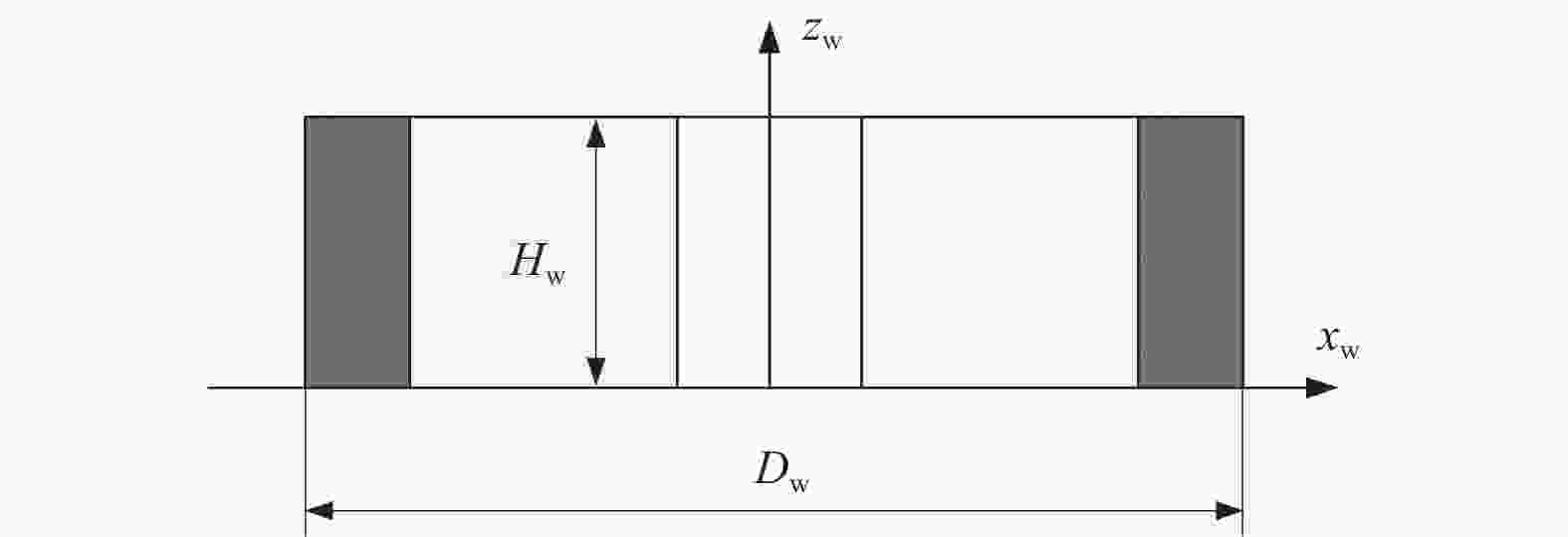
表 1 容屑槽几何参数

Table 1. Geometric parameters of flute

容屑槽几何参数	数值
螺旋角 β / (°)	30
径向前角 γ / (°)	5
芯径 d_c / mm	4
槽宽 φ / (°)	150

下载: 导出CSV

表 2 磨削加工实验参数

Table 2. Grinding parameters in experiments

实验组编号	砂轮线速度 v_s / (m·s⁻¹)	工件轴向进给速度 v_a / (mm·min⁻¹)	偏置 Δa_x / mm
1	18	60	0
2	18	90	0
3	24	60	0
4	24	90	0
5	18	70	1.2
6	22	90	0
7	20	90	1.2
8	24	70	0
9	18	80	0
10	22	60	1.2
11	20	60	0
12	24	80	1.2
13	18	60	0.8
14	22	80	0.4
15	20	80	0.8
16	24	60	0.4
17	18	90	0.4
18	22	70	0.8
19	20	70	0.4
20	24	90	0.8

下载: 导出CSV

参考文献(18)

[1]	宋铁军, 周志雄, 李伟, 等. 硬质合金立铣刀螺旋槽磨削表面粗糙度模型研究 [J]. 机械工程学报,2017,53(17):185-192. doi: 10.3901/JME.2017.17.185 SONG Tiejun, ZHOU Zhixiong, LI Wei, et al. Roughness model for helical flute of cemented carbide end mill under grinding [J]. China Mechanical Engineering,2017,53(17):185-192. doi: 10.3901/JME.2017.17.185
[2]	毕雪峰, 杨承三, 景璐璐. 深切缓进给磨削烧伤实验研究 [J]. 上海理工大学学报,2014,36(3):303-306. doi: 10.13255/j.cnki.jusst.2014.03.018 BI Xuefeng, YANG Chengsan, JING Lulu. Experimental research on grinding burn in creep feed grinding [J]. Journal of University of Shanghai for Science and Technology,2014,36(3):303-306. doi: 10.13255/j.cnki.jusst.2014.03.018
[3]	MENG Q Y, GUO B, ZHAO Q L, et al. Modelling of grinding mechanics: A review [J]. Chinese Journal of Aeronautics,2023,36(7):25-39. doi: 10.1016/j.cja.2022.10.006
[4]	宋铁军, 周志雄, 李伟, 等. 硬质合金刀具螺旋槽缓进给磨削力研究 [J]. 中国机械工程,2014,25(9):1153-1158. doi: 10.3969/j.issn.1004-132X.2014.09.004 SONG Tiejun, ZHOU Zhixiong, LI Wei, et al. Research on grinding forces of creep feed grinding cemented carbide tool helical grooves [J]. China Mechanical Engineering,2014,25(9):1153-1158. doi: 10.3969/j.issn.1004-132X.2014.09.004
[5]	赵延军, 钱灌文, 刘权威, 等. 砂轮刚性对磨削性能及产品加工质量的影响 [J]. 金刚石与磨料磨具工程,2017,37(1):56-60. doi: 10.13394/j.cnki.jgszz.2017.1.0011 ZHAO Yanjun, QIAN Guanwen, LIU Quanwei, et al. Influence of wheel stiffness on grinding performance and product machining quality [J]. Diamond & Abrasives Engineering,2017,37(1):56-60. doi: 10.13394/j.cnki.jgszz.2017.1.0011
[6]	SALATA M. The analysis of the influence of technological parameters on the grinding temperature in the single-pass grinding process of solid carbide end mill flutes [J]. Advances in Science and Technology-Research Journal,2022,16(1):190-202. doi: 10.12913/22998624/143483
[7]	DE PAYREBRUNE K M, KRÖGER M. Dynamical aspects in modeling long cantilevering workpieces in tool grinding [J]. Journal of Sound and Vibration,2015,355:407-417. doi: 10.1016/j.jsv.2015.06.027
[8]	DE PAYREBRUNE K M, KRÖGER M. An integrated model of tool grinding: challenges, chances and limits of predicting process dynamics [J]. Production Engineering,2016,10:421-432. doi: 10.1007/s11740-016-0687-2
[9]	DENKENA B, DITTRICH M A, BÖß V, et al. Self-optimizing process planning for helical flute grinding [J]. Production Engineering,2019,13:599-606. doi: 10.1007/s11740-019-00908-0
[10]	UHLMANN E, GÜLZOW B, MUTHULINGAM A. Optimising the grinding wheel design for flute grinding processes utilising numerical analysis of the complex contact conditions [J]. Journal of Machine Engineering,2020,20(3):85-94. doi: 10.36897/jme/119641
[11]	DITTRICH M A, BÖß V, WICHMANN M, et al. Simulation-based compensation of deflection errors in helical flute grinding [J]. CIRP Journal of Manufacturing Science and Technology,2020,28:136-143. doi: 10.1016/j.cirpj.2019.11.002
[12]	JEYARAJ D, LAHMANN H W, WELZEL F. A data-driven model to predict dressing interval during a multi-flute end mill grooving process using a multilayered diamond grinding wheel [J]. Procedia CIRP,2023,117:353-358. doi: 10.1016/j.procir.2023.03.060
[13]	WIESENER F, BERGMANN B, WICHMANN M, et al. Modeling of heat transfer in tool grinding for multiscale simulations [J]. Procedia CIRP,2023,117:269-274. doi: 10.1016/j.procir.2023.03.046
[14]	REN L, XU J, ZHANG XM, et al. Determination of wheel position in flute grinding of cylindrical end-mills considering tolerances of flute parameters [J]. Journal of Manufacturing Processes,2022,74:63-74. doi: 10.1016/j.jmapro.2021.11.065
[15]	MALKIN S, GUO CS. Grinding technology: Theory and application of machining with abrasives [M]. New York: Industrial Press, 2008.
[16]	CHEN X, ROWE W B, ALLANSON D R, et al. A grinding power model for selection of dressing and grinding conditions [J]. Journal of Manufacturing Science and Engineering,1999,121(4):632-637. doi: 10.1115/1.2833084
[17]	任磊, 韩家祥, 张新民, 等. 圆弧投影法在圆柱立铣刀容屑槽刃磨中的应用 [J]. 机械工程学报,2023,59(17):335-348. doi: 10.3901/JME.2023.17.335 REN Lei, HAN Jiaxiang, ZHANG Xinmin, et al. Application of circular arc projection method in flute grinding of cylindrical end-mills [J]. Journal of Mechanical Engineering,2023,59(17):335-348. doi: 10.3901/JME.2023.17.335
[18]	LIU X L, CHEN Z, JI W, et al. A compensation method for wheel wear in solid cutting tool groove grinding based on iteration algorithm [J]. The International Journal of Advanced Manufacturing Technology,2020,107:3389-3399. doi: 10.1007/s00170-020-05269-y