Simulation study of cutting fluid flow field in kerf of fine diameter diamond wire saw
-
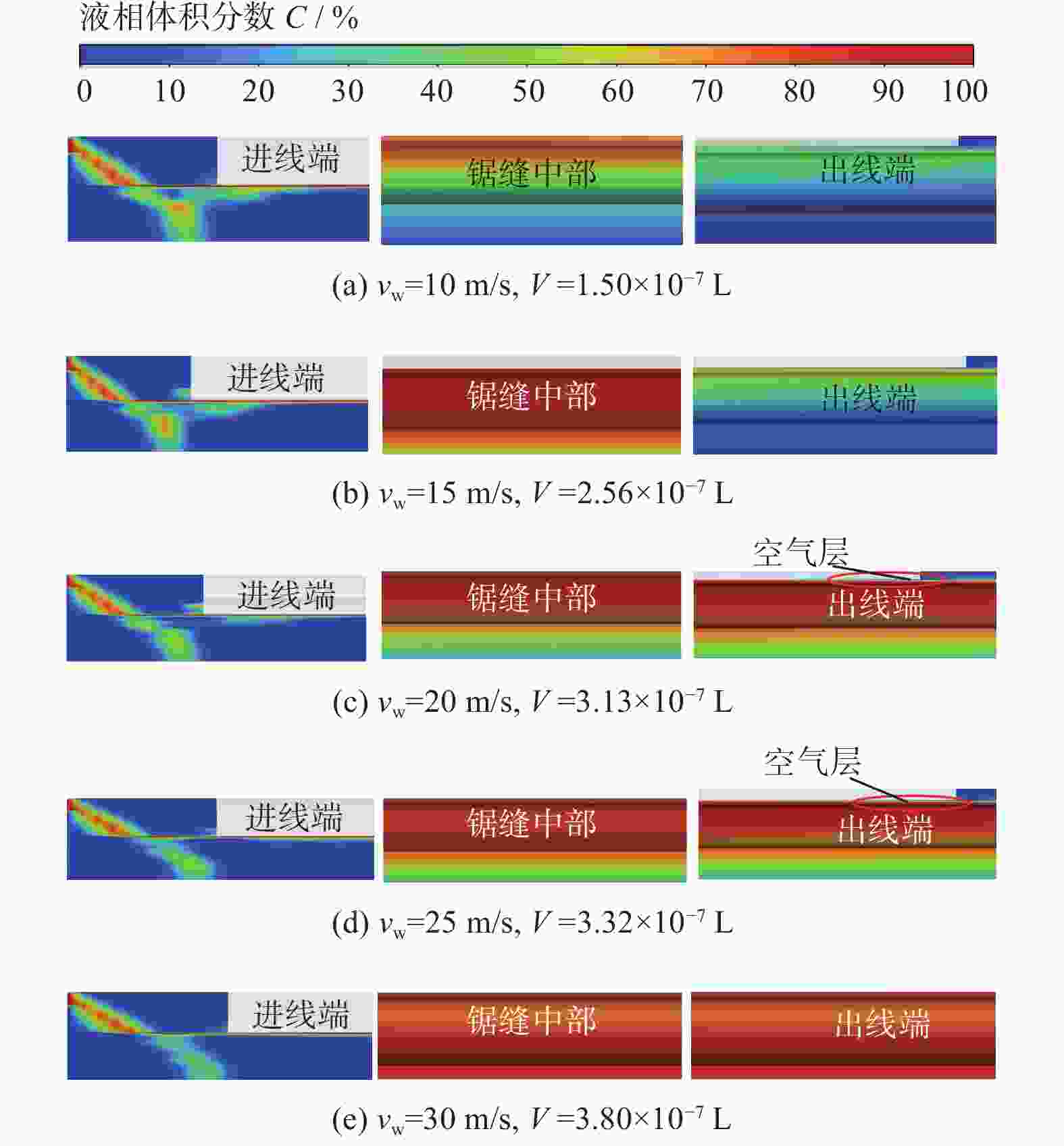
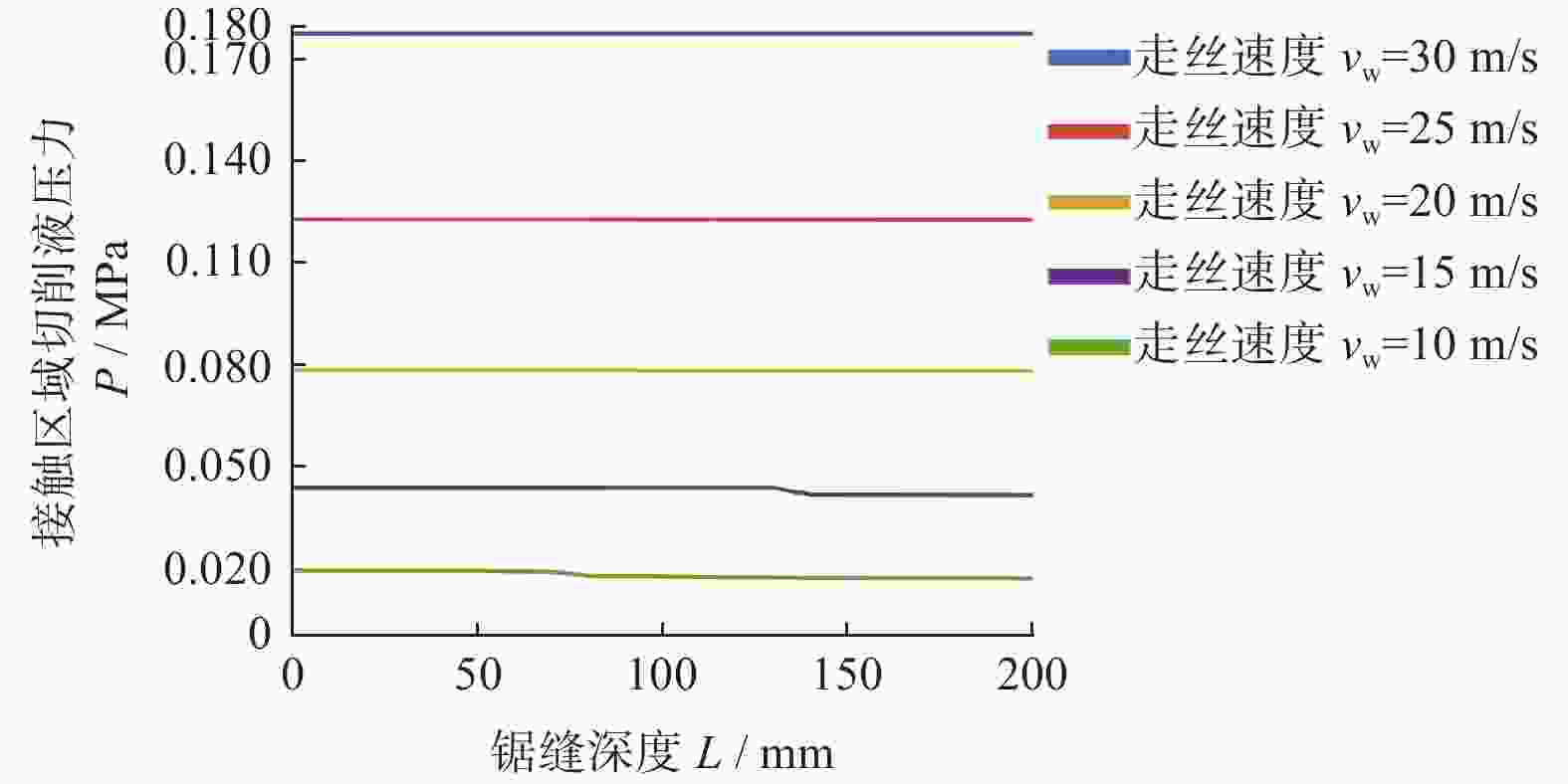
摘要: 随着工件大尺寸化及锯丝细线化,锯切加工过程中的锯缝越来越深且窄,切削液在锯切过程中无法充分发挥作用,对切片质量影响较大。基于计算流体力学(computational fluid dynamics,CFD)数值模拟,通过建立CFD锯缝模型,对金刚石线锯锯切加工材料时锯缝内切削液流场进行分析研究。仿真分析发现:在小尺寸锯缝内,随着走丝速度增大至25 m/s,切削液更能充分进入锯缝,在锯丝与工件接触区域及非接触区域充满液体后,接触区域流体压力在
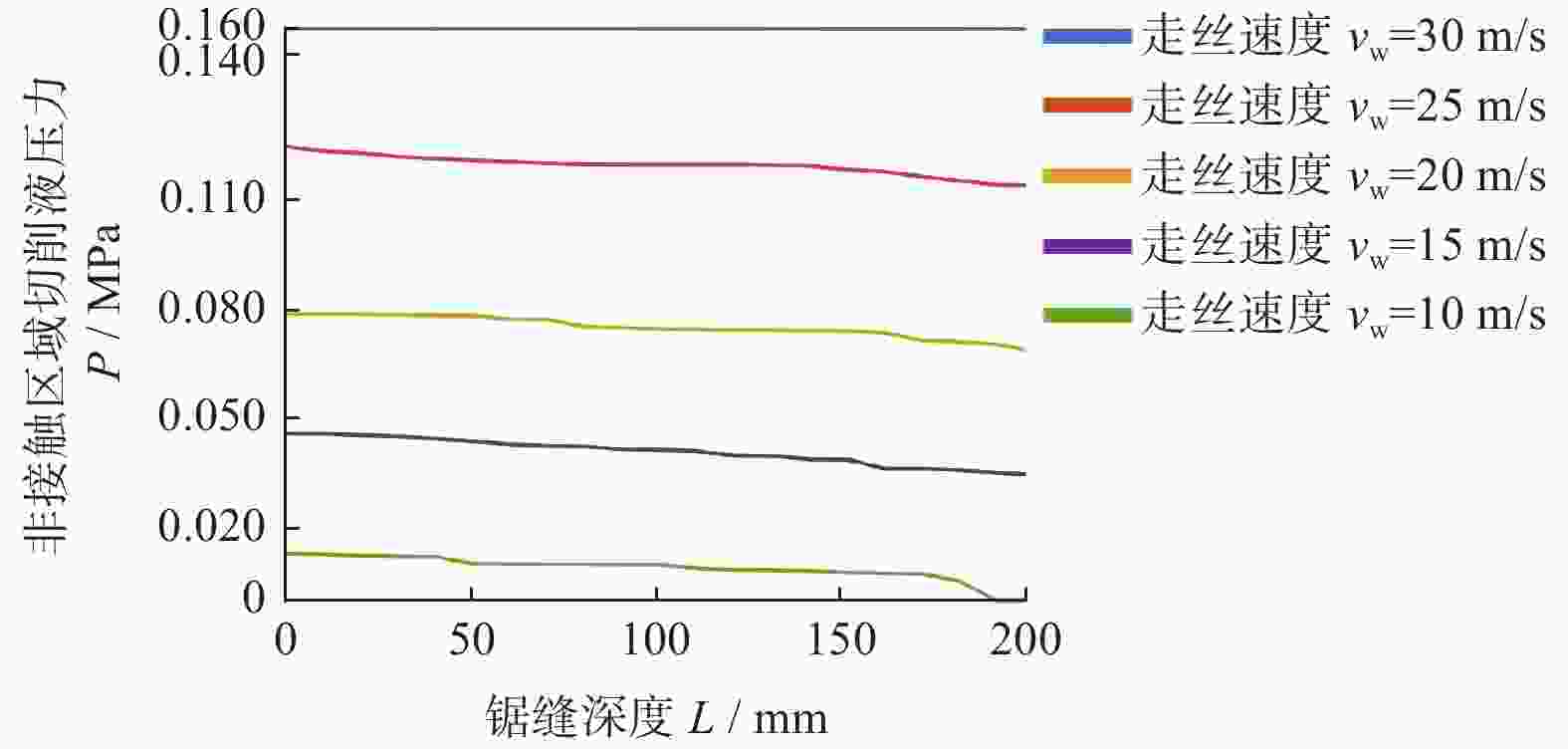
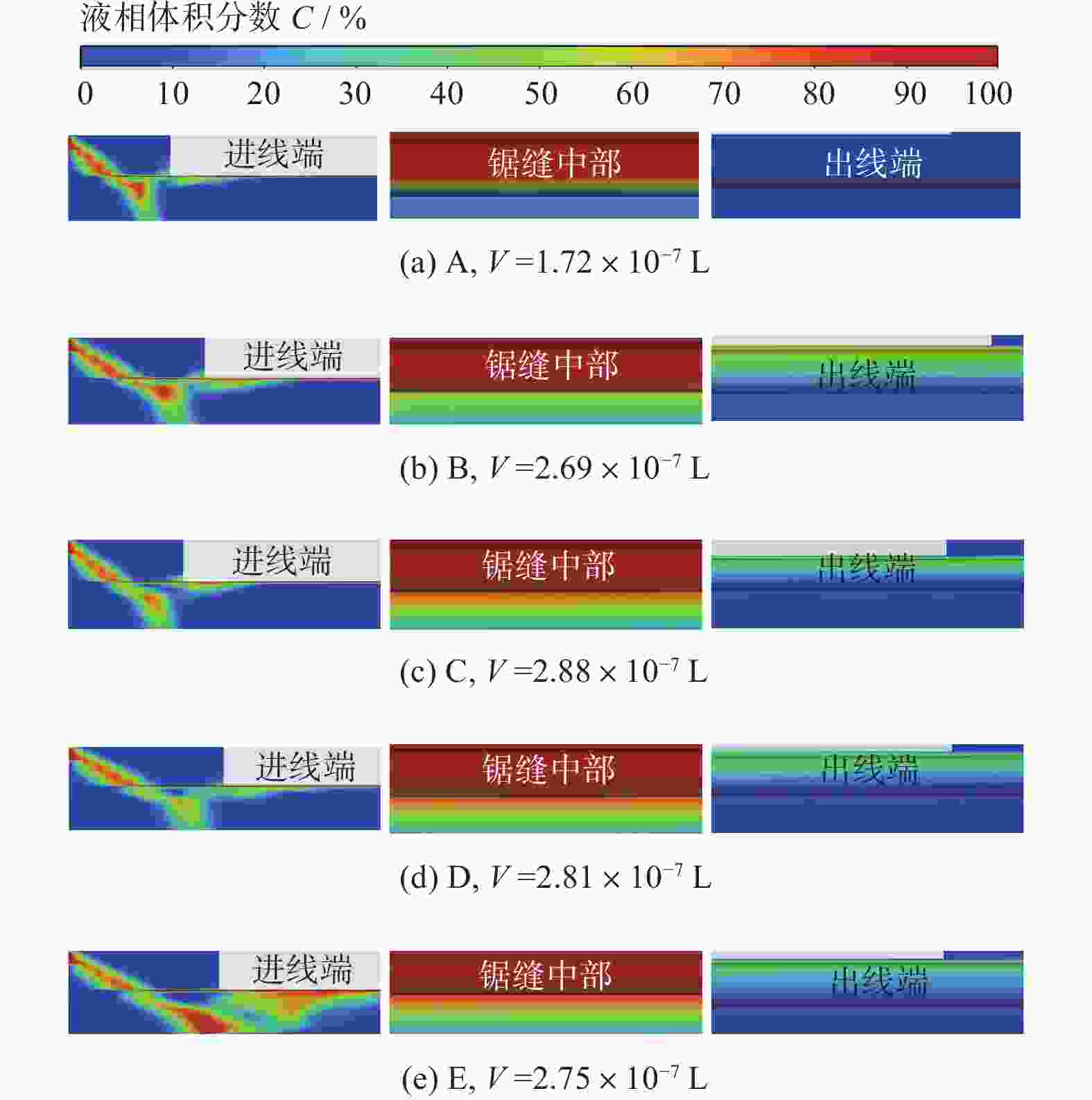
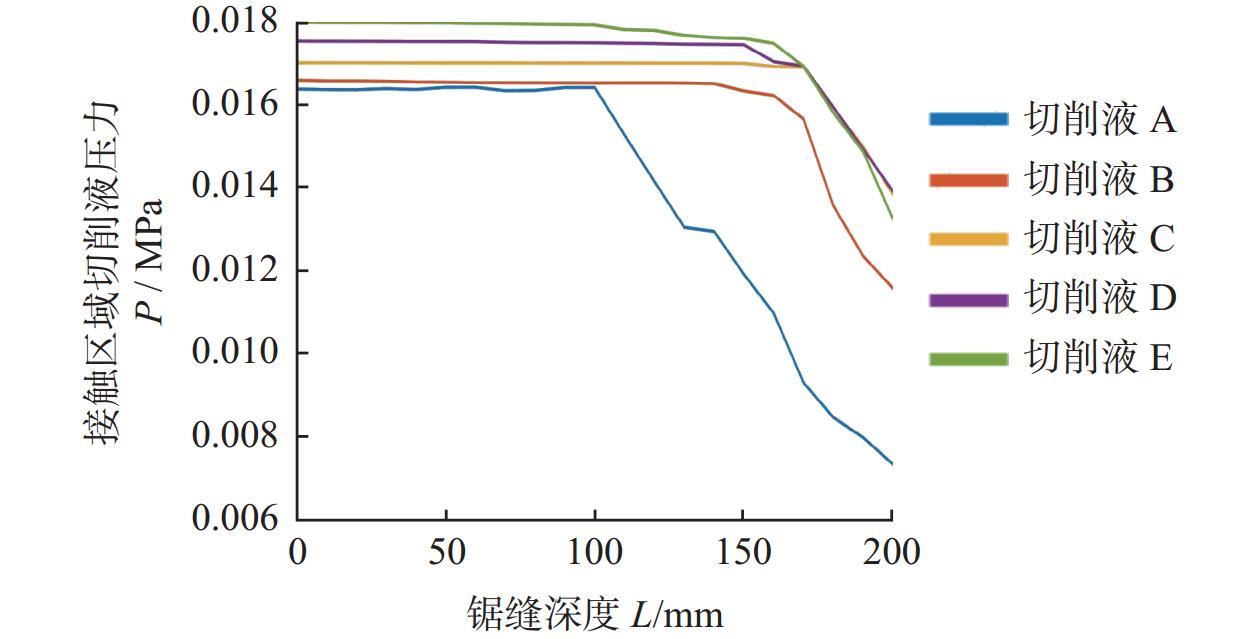
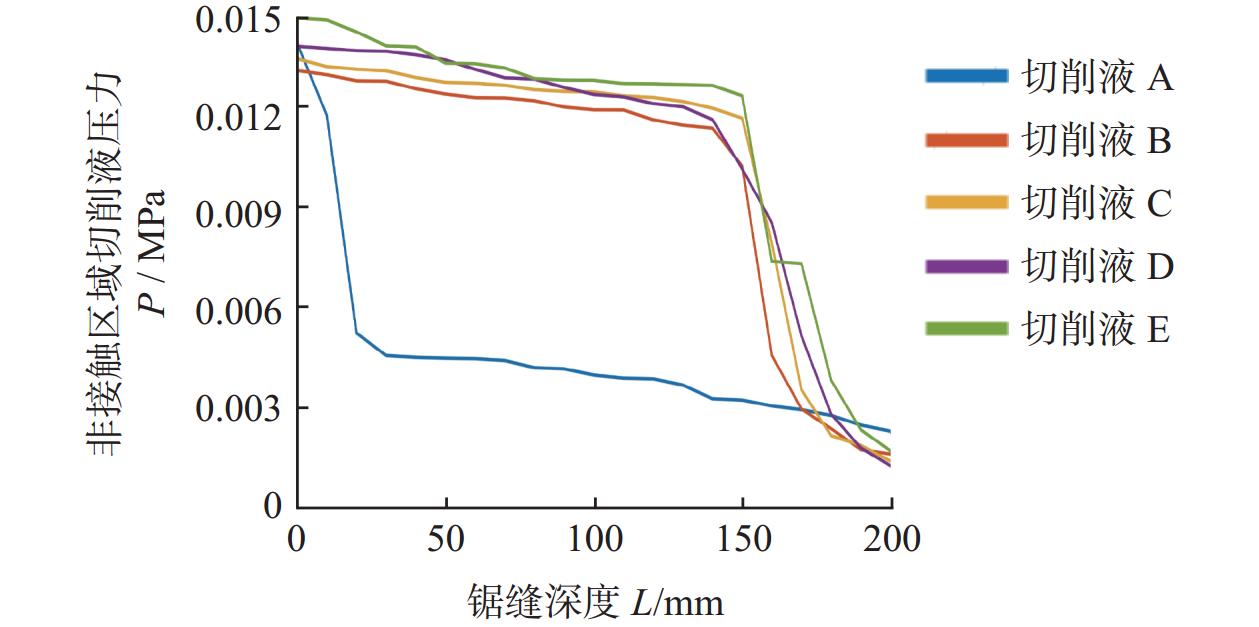
0.1790 MPa左右,非接触区域流体压力在0.1590 MPa左右;切削液黏度和表面张力在一定范围内的降低,有利于保证锯缝内切削液的相对饱和与稳定,同时可以使锯缝内切削液压力分布更为稳定。Abstract: Objectives: Electroplated diamond wire saws are widely used in the field of slicing hard and brittle materials such as monocrystalline silicon and sapphire. Cutting fluid should give full play to its role in the sawing process, which is conducive to the improvement of wafer quality. As the size of the wafer increases and the diameter of the wire saw decreases, the kerf in the sawing process becomes deeper and narrower, and the cutting fluid cannot enter the kerf in large quantities, resulting in worse lubrication and cooling effects during the sawing process, which leads to the decline of the surface quality of the wafer. Based on computational fluid dynamics (CFD) numerical simulation methods, the cutting fluid flow field in the cutting seam of the diamond wire saw was analyzed and studied. Methods: In this paper, based on CFD numerical simulation methods, the cutting fluid flow field in the sawing seam of the diamond wire saw is analyzed and studied. Firstly, according to the actual situation of the diamond wire saw cutting process, a 3D simulation geometric model is established based on the liquid supply mode, where cutting fluid flows along the sawing wire and is brought into the sawing area by the motion of the sawing wire. Heat transfer is not considered in this study, and the cutting fluid is assumed to be a viscous incompressible fluid. The governing equations of fluid flow include the continuity equation and the momentum equation. It is found from the equations that the main factors affecting the flow field distribution of cutting fluid in the kerf are wire speed and cutting fluid density. By calculating Reynolds number and Weber number, the fluid model studied in this paper is selected as the Transition SST model. The VOF method is determined to characterize the fluid state of cutting fluid in the saw joint, and the CSF model is introduced into the VOF method to characterize the influence of surface tension. Considering the influence of physical properties of cutting fluid, the density, viscosity, surface tension, and wall contact angle of cutting fluid are measured experimentally. The momentum equation is solved by a pressure-based solver, the continuity equation is solved by implicit time discretization, and the PISO method is used for pressure-velocity coupling. Result: With the increase of chip size and the decrease of wire saw diameter, the size of the saw seam is getting smaller and smaller. The main fluid entering the saw seam is shear flow, and the main factor affecting the fluid motion state is the wire speed. Under the condition of small-size sawing, when the wire speed is low (vw≤25 m/s), both the contact area and the non-contact area of the saw wire in the sawing joint are not completely filled with liquid, and the liquid volume fraction in the contact area is < 100%, with an air layer in the area. With the increase of wire speed, more and more cutting fluid enters the sawing joint. With the increase of wire speed, more and more cutting fluid enters the saw seam. When vw>25 m/s, both the contact area and the non-contact area are filled with liquid. The cutting fluid pressure in the saw seam increases with the increase of wire speed on both the contact area side and the non-contact area side, and the pressure difference on both sides also increases generally. The pressure distribution on both sides becomes more stable. After both sides of the saw seam are filled with liquid, the pressure on one side of the contact area is about0.1790 MPa, and the pressure on one side of the non-contact area is about0.1590 MPa. With the gradual reduction of the viscosity and surface tension of the cutting fluid, the cutting fluid gradually fills the saw joint. Howver, when the viscosity and surface tension of the cutting fluid are too small, the cutting fluid entering the saw joint will tend to decrease. The cutting fluid pressure in the saw seam increases with the decrease of the cutting fluid viscosity and surface tension in both the contact area and the non-contact area, and the pressure distribution becomes more stable. However, when the viscosity and the surface tension are too small, the pressure will also fluctuate. Under the physical properties of the cutting fluid C, with a density of 872.5 kg·m−3, viscosity of 1.15 mPa·s and surface tension of 34.02 mN·m−1, the pressure distribution of the cutting fluid on the contact area side and the non-contact area side is more stable. The maximum pressure on the contact area side is about0.0169 MPa, and the maximum pressure on the non-contact area side is about0.0132 MPa. Conclusions: (1) Under small sawing sizes, when the wire speed is low, the cutting fluid is difficult to fully enter the sawing area to play its role. With the increase of the wire speed (vw>25 m/s), the contact area and non-contact area between the saw wire and the workpiece are gradually filled with liquid, and the cutting fluid pressure and pressure difference between the contact area and the non-contact area show an overall increasing trend. When the contact area and non-contact area are full of cutting fluid, the cutting fluid pressure distribution in the saw joint is relatively stable, with the pressure in the contact area being about0.1790 MPa and the pressure in the non-contact area being about0.1590 MPa. (2) The reduction of liquid viscosity and surface tension within a certain range is conducive to ensuring the relative saturation and stability of the cutting fluid in the saw joint, and at the same time, it can make the pressure distribution of the cutting fluid in the saw joint more stable. A comprehensive comparison of the physical properties of the 5 groups of cutting fluids shows that the physical properties of the cutting fluid C during the diamond line saw cutting process are more conducive to its entry into the saw joint. -
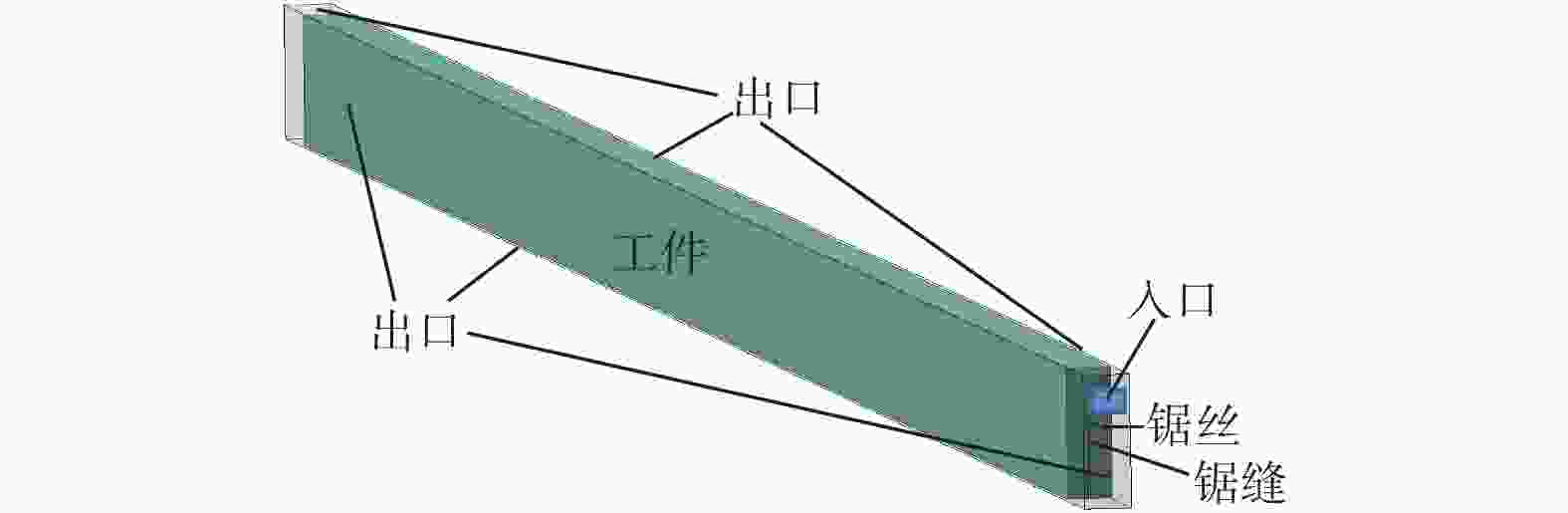
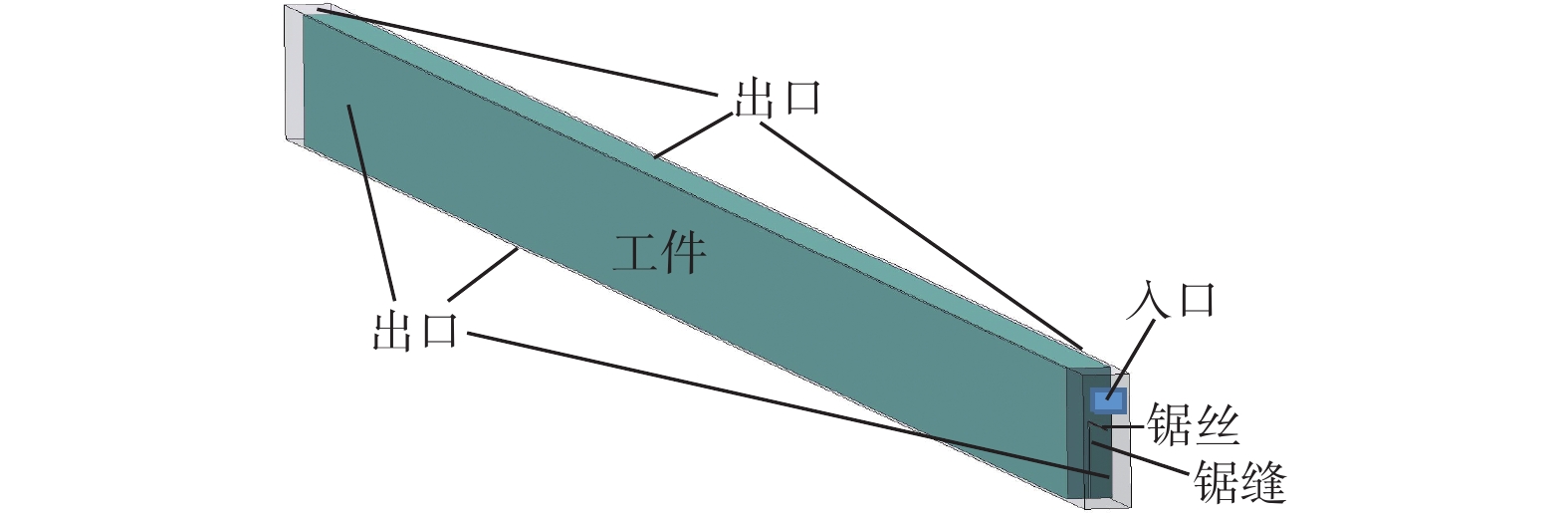
表 1 锯缝流场仿真几何模型参数
Table 1. Parameters of geometrical model for kerf flow field simulation
参数 取值 锯缝长度 l / mm 210 芯线直径 dw / μm 36 锯缝宽度 Dw / μm 60 锯丝张紧力 F / N 5.8 表 2 网格独立性验证结果
Table 2. Results of grid independence verification
网格数量 N 压力 P / Pa 相对误差 S / % 3 518 680 9 000 — 4 286 064 9 300 3.33 5 581 660 9 150 1.67 表 3 切削液物理属性
Table 3. Physical properties of cutting fluid
切削液 密度
ρ/(kg·m−3)黏度
Μ/(mPa·s)表面张力
γ/(mN·m−1)与单晶硅表面
接触角θ1/(°)与锯丝表面
接触角θ2/(°)A 840.0 1.26 38.57 30 51 B 850.5 1.20 36.06 27 37 C 872.5 1.15 34.02 20 33 D 900.3 1.12 33.08 13 21 E 921.5 1.08 30.35 11 13 表 4 边界条件
Table 4. Boundary conditions
区域 类型 参数 入口 速度入口 速度为1.5 m/s,面积为1.5 mm × 0.4 mm 出口 压力出口 表面压力为0 工件外表面 固定壁面 无滑移 锯缝内表面 固定壁面 无滑移 锯丝表面 移动壁面 无滑移,速度为10~30 m/s -
[1] 葛培琪, 陈自彬, 王沛志. 单晶硅切片加工技术研究进展 [J]. 金刚石与磨料磨具工程,2020,40(4):12-18. doi: 10.13394/j.cnki.jgszz.2020.4.0002GE Peiqi, CHEN Zibin, WANG Peizhi. Review of monocrystalline silicon slicing technology [J]. Diamond & Abrasives Engineering,2020,40(4):12-18. doi: 10.13394/j.cnki.jgszz.2020.4.0002 [2] BHAGAVAT S, KAO I. A finite element analysis of temperature variation in silicon wafers during wiresaw slicing [J]. International Journal of Machine Tools and Manufacture,2008,48(1):95-106. doi: 10.1016/j.ijmachtools.2007.07.009 [3] MÖLLER H J. Basic mechanisms and models of multi-wire sawing [J]. Advanced Engineering Materials,2004,6(7):501-513. doi: 10.1002/adem.200400578 [4] ZHU L Q, KAO I. Galerkin-based modal analysis on the vibration of wire–slurry system in wafer slicing using a wiresaw [J]. Journal of Sound and Vibration,2005,283(3/4/5):589-620. doi: 10.1016/j.jsv.2004.04.018 [5] GE P Q, SANG B, GAO Y F. The numerical analysis on action mechanism of slurry in free abrasive wiresaw slicing [J]. Key Engineering Materials,2007(359/360):455-459. doi: 10.4028/www.scientific.net/KEM.359-360.455 [6] ISHIKAWA K I, SUWABE H, ITOH S I, et al. A basic study of the behavior of slurry action at multi-wire saw [J]. Key Engineering Materials,2003(238/239):89-92. doi: 10.4028/www.scientific.net/KEM.238-239.89 [7] NASSAUER B, HESS A, KUNA M. Numerical and experimental investigations of micromechanical processes during wire sawing [J]. International Journal of Solids and Structures,2014,51(14):2656-2665. doi: 10.1016/j.ijsolstr.2014.03.040 [8] 林麟. 磨粒线切割中的流体行为研究[D]. 厦门: 华侨大学, 2020.LIN Lin. Study on fluid behavior in abrasive wire cutting [D]. Xiamen: Huaqiao University, 2020. [9] 郑忠利. 静电喷雾金刚石线锯切割液吸附特性及切割实验研究[D]. 杭州: 浙江工业大学, 2020.ZHENG Zhongli. Adsorption characteristics and cutting experiments of electrostatic spray diamond wire saw cutting fluid [D]. Hangzhou: Zhejiang University of Technology, 2020. [10] QIU J, LI X F, ZHANG S B. Research on an improved bath cooling and lubrication method for diamond wire sawing [J]. The International Journal of Advanced Manufacturing Technology,2021,112:1-10. doi: 10.1007/s00170-020-06195-9 [11] 施郁虎. 基于金刚石线锯的微量润滑与工艺研究[D]. 镇江: 江苏科技大学, 2020.SHI Yuhu. Micro lubrication and process research based on diamond wire saw [D]. Zhenjiang: Jiangsu University of Science and Technology, 2020. [12] 宁培桓, 周建伟, 刘玉岭, 等. Si单晶片切削液挂线性能的研究 [J]. 半导体技术,2008,33(11):981-984. doi: 10.3969/j.issn.1003-353X.2008.11.011NING Peihuan, ZHOU Jianwei, LIU Yuling, et al. Study on the capability of adhesion of monocrystalline Si wafer cutting fluid [J]. Semiconductor Technology,2008,33(11):981-984. doi: 10.3969/j.issn.1003-353X.2008.11.011 [13] 冯勇, 王晓宇, 徐振钦. 单晶硅料摆辅助多金刚线切片的锯切力模型研究 [J]. 机械工程学报,2021,57(19):260-272. doi: 10.3901/JME.2021.19.260FENG Yong, WANG Xiaoyu, XU Zhenqin. Research on cutting force model of diamond wire saw with single crystal silicon swing [J]. Journal of Mechanical Engineering,2021,57(19):260-272. doi: 10.3901/JME.2021.19.260 [14] 章梓雄, 董曾南. 黏性流体力学[M]. 北京: 清华大学出版社, 2011.ZHANG Zixiong, DONG Zengnan. Viscous fluid mechanics [M]. Beijing: Tsinghua University Press, 2011. [15] 任玉新, 陈海昕. 计算流体力学基础[M]. 北京: 清华大学出版社, 2006.REN Yuxin, CHEN Haixin. Fundamentals of computational fluid dynamics [M]. Beijing: Tsinghua University Press, 2006. [16] L·普朗特. 流体力学概论[M]. 郭永怀, 陆士嘉, 译. 北京: 科学出版社, 1984.L PRANDTL. Introduction to fluid mechanics [M]. GUO Yonghuai, LU Shijia, translated. Beijing: Science Press, 1984. [17] 雷娟棉, 谭朝明. 基于Transition SST模型的高雷诺数圆柱绕流数值研究 [J]. 北京航空航天大学学报,2017,43(2):207-217. doi: 10.13700/j.bh.1001-5965.2016.0098LEI Juanmian, TAN Zhaoming. Numerical simulation for flow around circular cylinder at high Reynolds number based on Transition SST model [J]. Journal of Beijing University of Aeronautics and Astronautics,2017,43(2):207-217. doi: 10.13700/j.bh.1001-5965.2016.0098 -



 下载:
下载:



 邮件订阅
邮件订阅 RSS
RSS
