聚晶金刚石层厚度与复合片直径对PDC残余热应力的影响

杨添添; 黄凯

doi:10.13394/j.cnki.jgszz.2023.0201

聚晶金刚石层厚度与复合片直径对PDC残余热应力的影响

doi: 10.13394/j.cnki.jgszz.2023.0201

杨添添,
黄凯^,

北京科技大学冶金与生态工程学院, 北京 100083

详细信息

通讯作者:
黄凯，男，1974年生，博士、副教授。主要研究方向：有色冶金。E-mail: khuang@metall.ustb.edu.cn

中图分类号: TQ163
计量
- 文章访问数: 22
- HTML全文浏览量: 13
- PDF下载量: 1
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-18
- 修回日期: 2024-01-20
- 录用日期: 2024-01-30
- 刊出日期: 2024-12-06

Effect of thickness of polycrystalline diamond layer and diameter of compact on residual thermal stress of PDC

YANG Tiantian,
HUANG Kai^,

School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing 100083, China

摘要

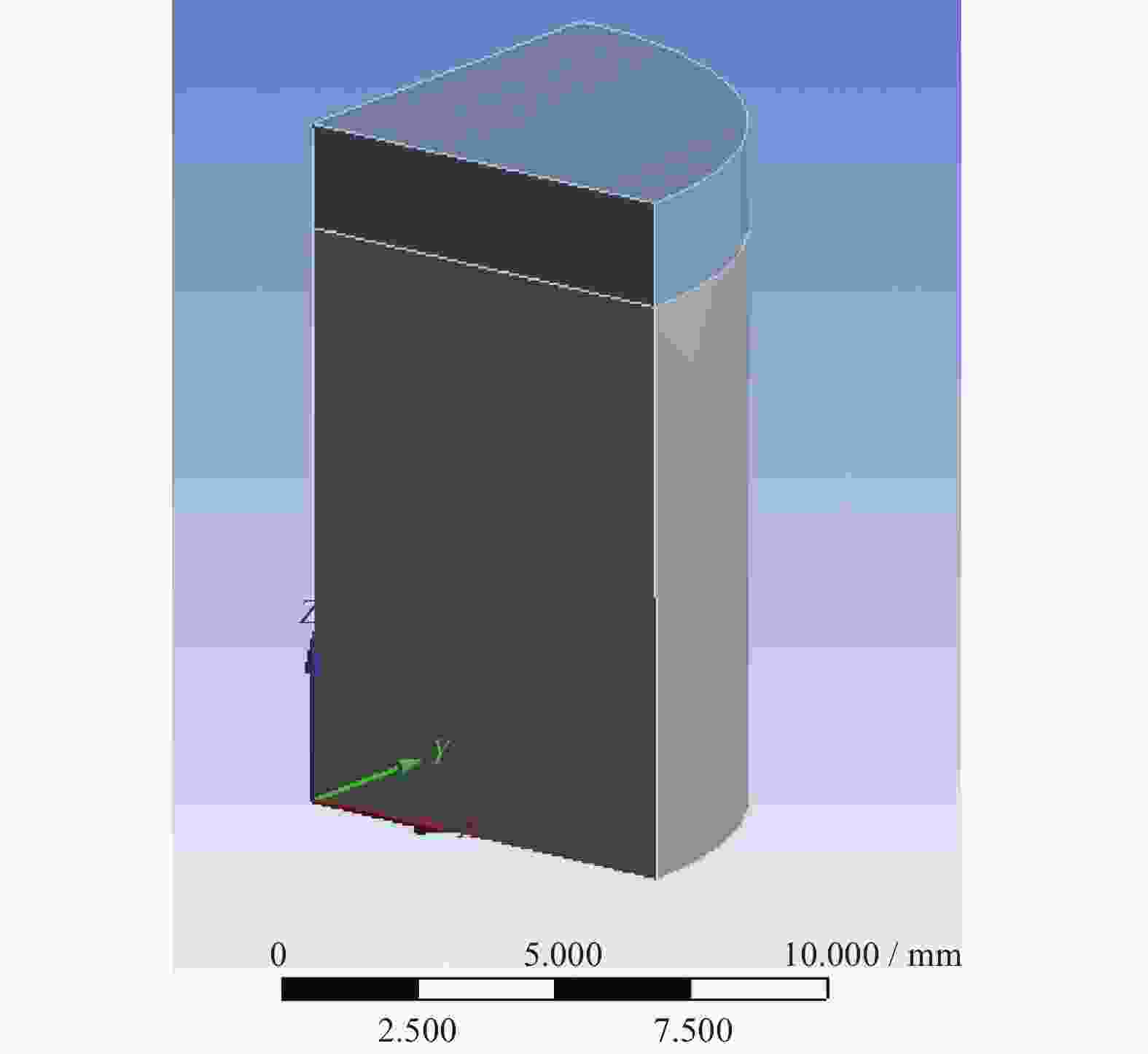
摘要: 残余热应力是导致聚晶金刚石复合片（PDC）失效的原因之一。为提升PDC在实际使用过程中的性能，并为PDC的设计提供模拟计算依据，利用ANSYS建立PDC的参数模型，通过“热-结构”耦合法计算PDC的残余热应力值，分析PCD层和硬质合金层的厚度比及PDC直径对残余热应力分布特征的影响规律。结果表明：当PDC直径为16 mm、总厚度为13 mm时，其PCD层和硬质合金层的最佳厚度比为0.180；当PCD层厚度为2.0 mm时，PDC最佳直径值为18 mm；当PCD层厚度为3.0 mm时，应根据实际使用情况确定PDC最佳直径值。
- 有限元分析 /
- 聚晶金刚石复合片 /
- 残余热应力 /
- 聚晶金刚石层厚度 /
- PDC直径
Abstract: Objectives: Polycrystalline diamond compact (PDC) is an ultra-high hardness composite material made from polycrystalline diamond (PCD) and cemented carbide through high temperature and high pressure sintering. PDC is widely used in oil and gas extraction, geothermal development, and coal field drilling. As drilling goes deeper, the formation pressure increases, and the geological rock layers become denser, harder, and more abrasive. Therefore, the comprehensive performance requirements for the drill bit and PDC are increasingly high. The presence of residual thermal stress can significantly weaken the performance of PDC, causing the PCD layer to fracture and detach, which is one of the important factors leading to the premature failure of PDC. Previous research methods for determining the residual thermal stress in PDC have certain limitations. Finite element simulation calculations can effectively compensate for these shortcomings. Therefore, this paper uses the ANSYS Workbench software to calculate and analyze the influence of the thickness ratio of the PCD layer to the cemented carbide layer in PDC and the diameter of PDC on residual thermal stress, providing references for the optimization of PDC design and performance improvement. Methods: ANSYS is one of the most commonly used finite element analysis software, which can effectively integrate multiple disciplines such as structural dynamics, thermodynamics, and fluid dynamics for simulation calculations. Using ANSYS, the model of PDC (assuming that temperature does not affect the physical properties of materials) can be established, and the residual thermal stress of PDC can be analyzed using the thermo-mechanical coupling method (which solves the impact of the temperature field on stress, strain, and displacement in the structure). The specific calculation process in this study is as follows: (1) Select the calculation method for steady-state temperature field and structural mechanics field coupling. (2) Establish the geometric model of PDC. According to the axisymmetric characteristics of PDC, establish its 1/4 structure to save computational space. (3) Define the physical and mechanical properties of the PCD layer and the cemented carbide layer, and then perform mesh division. (4) Set boundary conditions and loads, using the temperature difference as the load, setting the reference temperature including the stress relaxation temperature of PDC, the axisymmetric boundary conditions of the model, as well as the heat convection boundary conditions between the outer surface of PDC and the air. (5) Perform result calculation and analysis. Results: Using the software to simulate the calculation of the residual thermal stress value and distribution during the unloading and cooling process of PDC, the following conclusions can be drawn: (1) The ANSYS simulation calculation shows that when the diameter of PDC is 16 mm and the total thickness is 13 mm, the optimal thickness of the PCD layer is 2.0 mm; (2) When the PCD layer thickness is 2.0 mm, the diameter of the composite piece can be selected as 18 mm, and the residual thermal stress of this specification of PDC is at the best value in the calculated range. When the PCD layer thickness is 3.0 mm, it cannot be decided based on a single residual thermal stress influence; this must rely on the specific application situation and the load condition, with a comprehensive consideration of the influence of the four residual thermal stresses; (3) The point of PDC diameter of 17 mm is one of the many fluctuation points, which may be a critical point. At this time, the radial displacement of the interface far from the center axis of PDC changes abruptly, causing the deflection of the entire PDC to change, and the axial tensile stress at the edge of the interface changes. Conclusion: The finite element calculation method can intuitively and clearly simulate the value and distribution of residual thermal stress during the unloading and cooling process of PDC, and effectively avoid the shortcomings of other experimental tests. It can provide useful ideas and suggestions for the design of PDC by analyzing the influence of the two appearance sizes, composite layer thickness, and diameter on the residual thermal stress of PDC, and drawing relevant conclusions. Based on the outstanding results in the simulation calculation, the conclusions obtained are tested by experiments to ensure the reliability of the final results.
- finite element analysis /
- polycrystalline diamond compact /
- residual thermal stress /
- composite layer thickness /
- diameter of the PDC

HTML全文

图 1 PDC计算模型

Figure 1. Computing model of PDC

下载: 全尺寸图片幻灯片

图 2 PCD层厚度为2.0 mm的PDC残余热应力分布图

Figure 2. Residual thermal stress distribution of PDC (PCD layer thickness is 2.0 mm)

下载: 全尺寸图片幻灯片

图 3 PCD层残余热应力随厚度比的变化

Figure 3. Residual thermal stress of PCD layer varies in accordance with thickness ratio

下载: 全尺寸图片幻灯片

图 4 PCD层残余热应力随PDC直径的变化（PCD层厚度为2.0 mm）

Figure 4. Residual thermal stress of PCD layer varies in accordance with PDC diameter （PCD layer thickness is 2.0 mm）

下载: 全尺寸图片幻灯片

图 5 PCD层残余热应力随PDC直径的变化曲线（PCD层厚度为3.0 mm）

Figure 5. Residual thermal stress of PCD layer varies in accordance with PDC diameter （PCD layer thickness is 3.0 mm）

下载: 全尺寸图片幻灯片

表 1 PDC材料物理性质^[12]

Table 1. Physical properties of PDC materials^[12]

物理指标	PCD层	硬质合金层
密度 ρ / (kg·m⁻³)	3 510	15 000
导热系数 (20 ℃) λ / (W·m⁻¹·℃⁻¹)	543	100
比热容 (20 ℃) c / (J·kg⁻¹·℃⁻¹)	790	230
热膨胀系数 (20 ℃) a / K⁻¹	2.5× 10⁻⁶	5.2× 10⁻⁶
弹性模量 E / GPa	890	579
泊松比 ν	0.07	0.22

下载: 导出CSV

表 2 PDC最大残余热应力计算值

Table 2. Maximum residual thermal stress of PDC

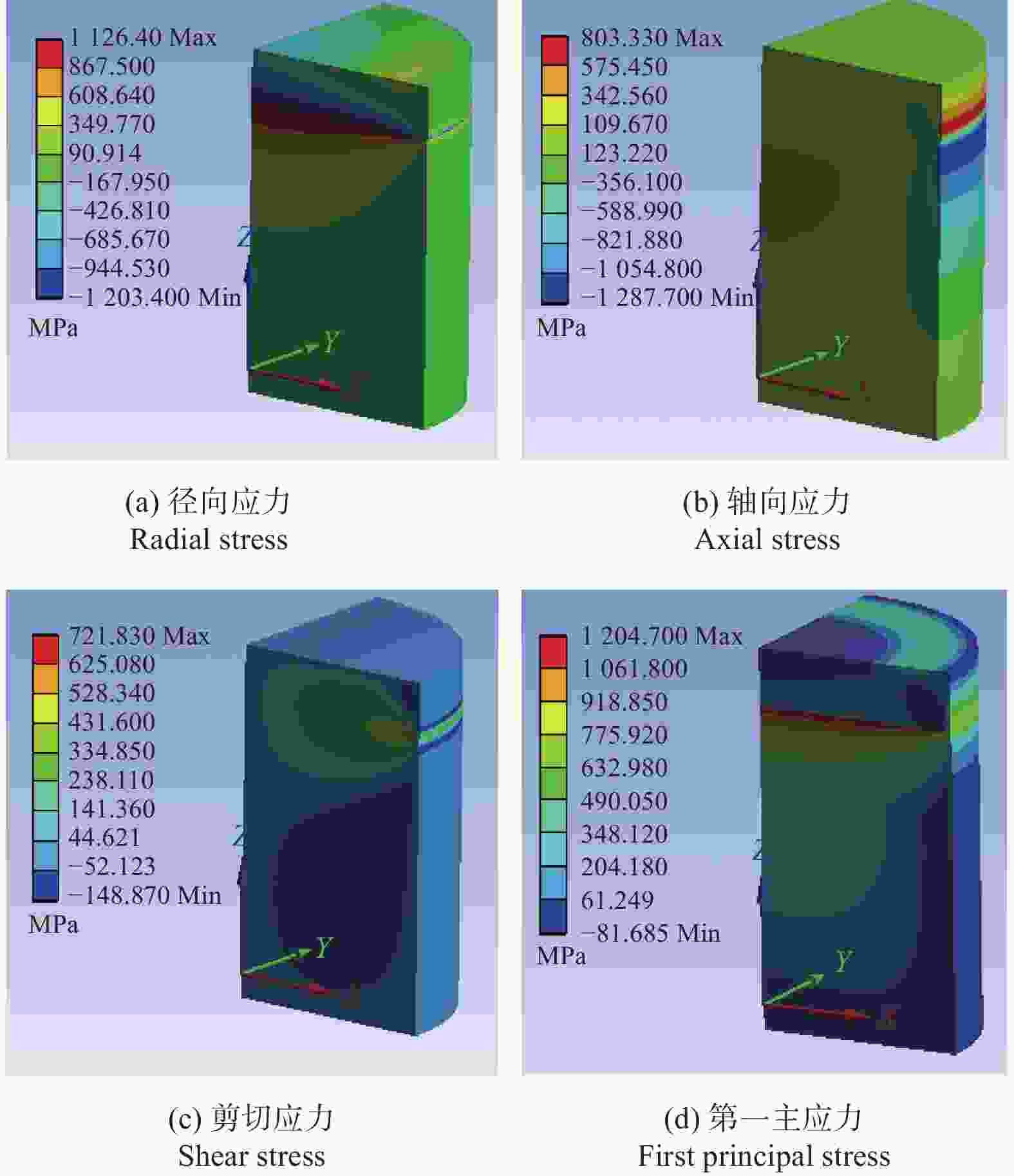
位置	径向应力极值 σ_xmax / MPa	轴向应力极值 σ_zmax / MPa	剪切应力极值 σ_xzmax / MPa	第一主应力 σ_first / MPa
PCD层	−1 203/400	−486/808	−1 309/722	842
硬质合金层	−217/1 126	−1 288/406	−1 489/718	1 205

下载: 导出CSV

表 3 PCD层和硬质合金层不同厚度比的PCD层残余热应力极大值

Table 3. Maximum residual thermal stress of PCD layer with different thickness ratio

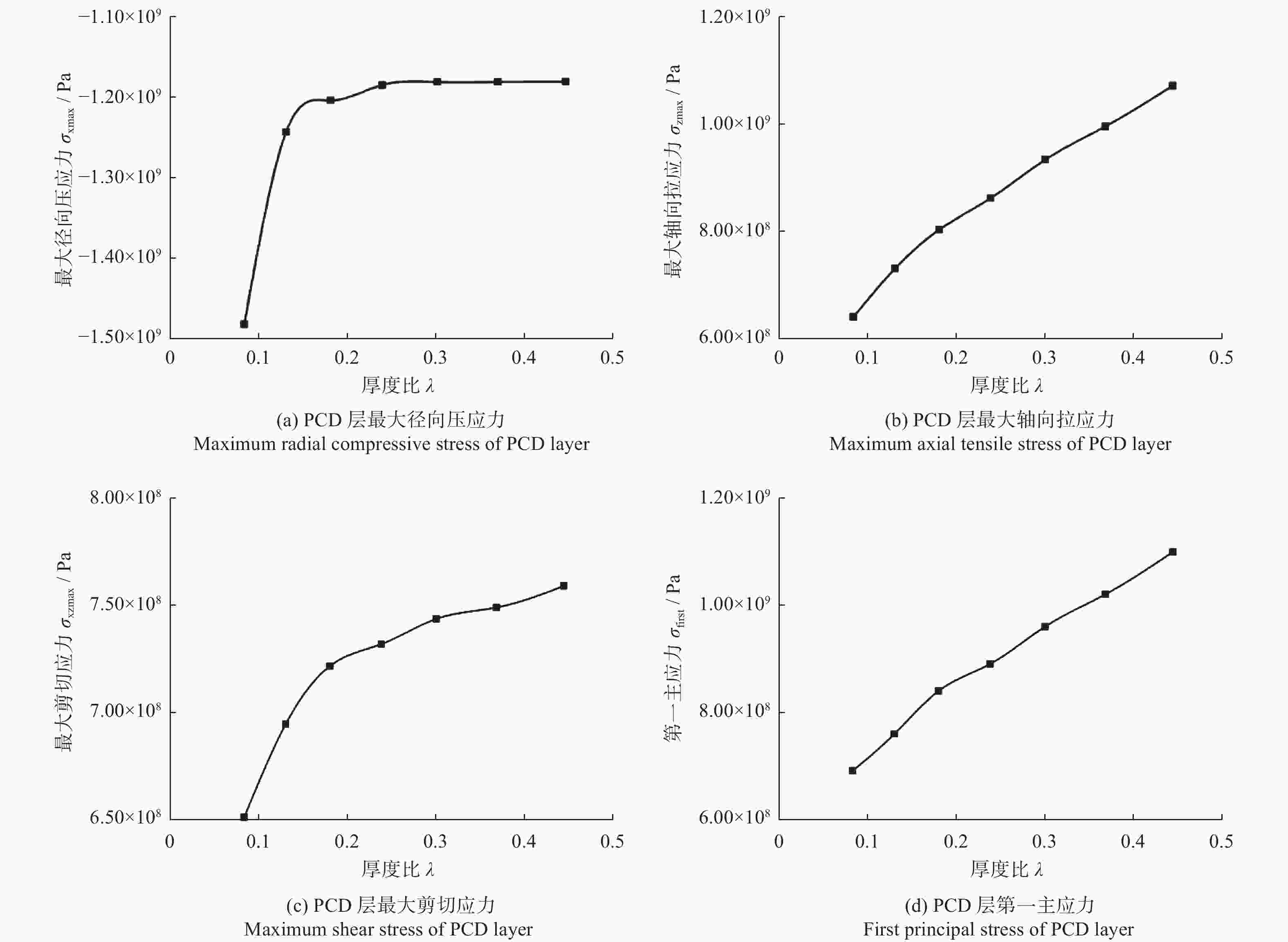
厚度比 λ	PCD层厚度 h / mm	径向压应力极大值 σ_xmax / MPa	轴向拉应力极大值 σ_zmax / MPa	剪切应力极大值 σ_xzmax / MPa	第一主应力 σ_first / MPa
0.083	1.0	−1 480	640	651	694
0.130	1.5	−1 240	731	693	768
0.180	2.0	−1 202	808	722	842
0.238	2.5	−1 184	862	732	892
0.300	3.0	−1 179	934	744	961
0.368	3.5	−1 180	996	749	1 021
0.444	4.0	−1 180	1 070	759	1 095

下载: 导出CSV

表 4 不同PDC直径的PCD层残余热应力极值

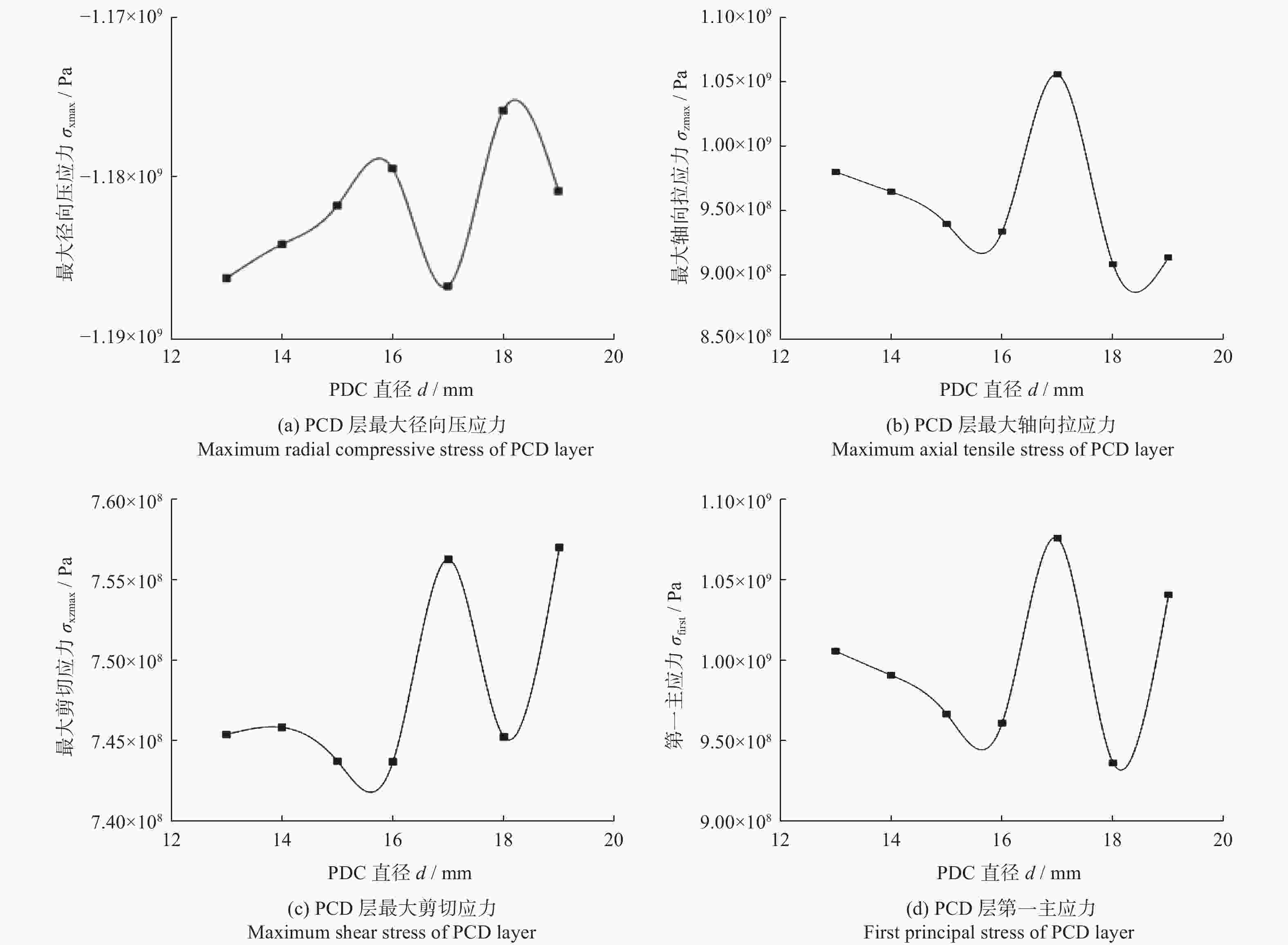
Table 4. Maximum residual thermal stress of PCD layer with different diameter

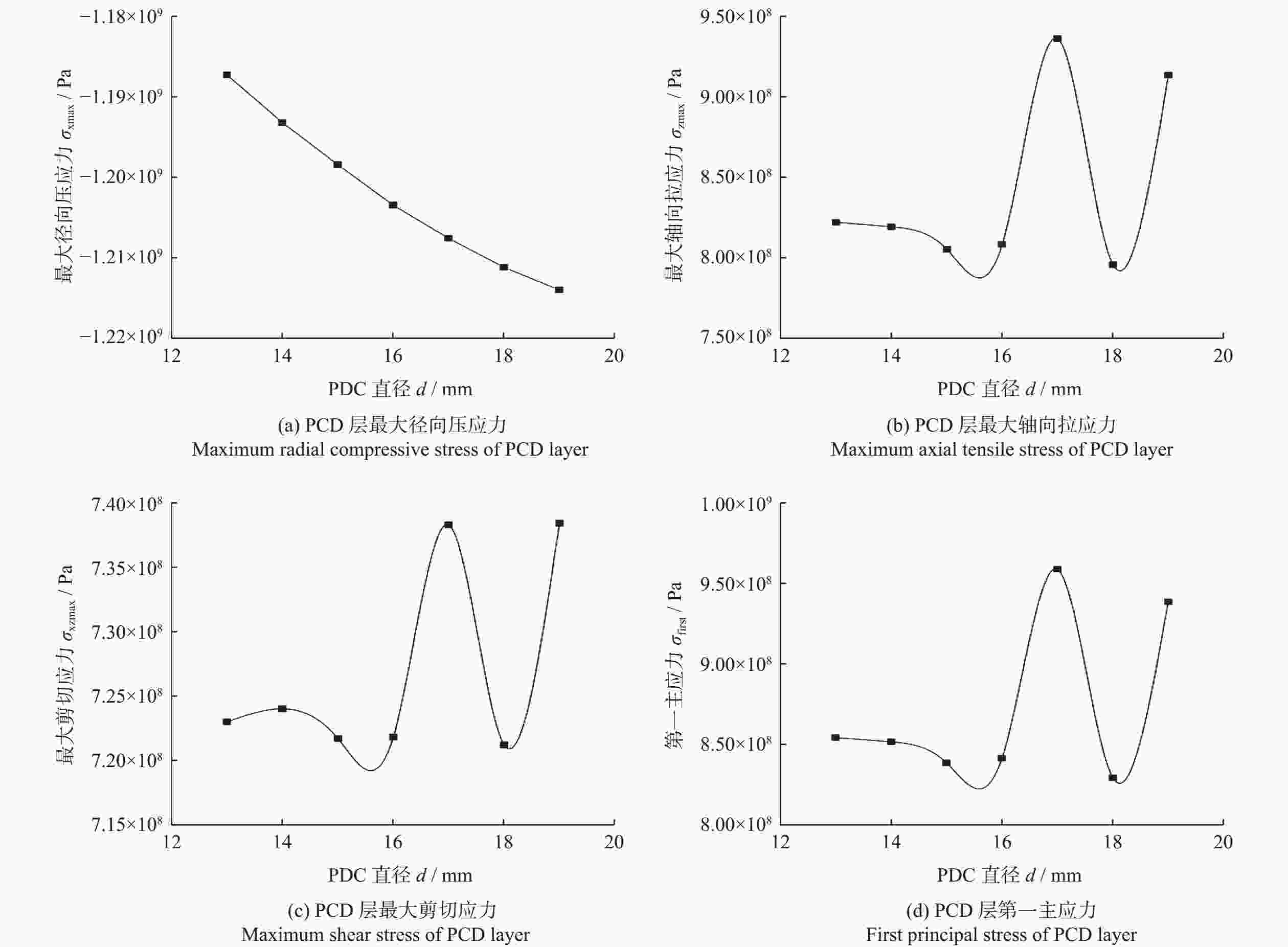
PDC直径 d / mm	径向压应力极大值 σ_xmax / MPa	轴向拉应力极大值 σ_zmax/ MPa	剪切应力极大值 σ_xzmax / MPa	第一主应力 σ_first / MPa
13	−1 187	822	723	854
14	−1 193	819	724	852
15	−1 198	805	722	839
16	−1 203	808	722	842
17	−1 207	936	738	959
18	−1 211	796	721	829
19	−1 214	914	738	939
20	−1 216	920	737	944

下载: 导出CSV

参考文献(13)

[1]	聂孟杰, 裴夤崟, 黄成志, 等. PDC性能优化及其钎焊技术研究现状 [J]. 电焊机,2023,53(4):63-72. doi: 10.7512/j.issn.1001-2303.2023.04.07 NIE Mengjie, PEI Yinyin, HUANG Chengzhi, et al. Research status of performance optimization of polycrystalline diamond compact [J]. Electric Welding Machine,2023,53(4):63-72. doi: 10.7512/j.issn.1001-2303.2023.04.07
[2]	杨金华, 郭晓霞. PDC钻头技术发展现状与展望 [J]. 石油科技论坛,2018,37(1):33-38. doi: 10.3969/j.issn.1002-302x.2018.01.008 YANG Jinhua, GUO Xiaoxia. The present status and outlook of PDC bit technology [J]. Oil Forum,2018,37(1):33-38. doi: 10.3969/j.issn.1002-302x.2018.01.008
[3]	秦文广, 刘瑞卿, 邹德良. 油气开采用PDC复合片的开发现状与发展趋势 [J]. 硬质合金,2023,40(4):310-318. doi: 10.3969/j.issn.1003-7292.2023.04.009 QIN Wenguang, LIU Ruiqing, ZOU Deliang. Status and trend of development of PDC composite for oil and gas exploration [J]. Cemented Carbides,2023,40(4):310-318. doi: 10.3969/j.issn.1003-7292.2023.04.009
[4]	宋晨杰, 魏文亮, 汪锦杰, 等. 钴粉形貌对聚晶金刚石复合片性能的影响 [J]. 金刚石与磨料磨具工程,2023,43(4):489-496. doi: 10.13394/j.cnki.jgszz.2022.0216 SONG Chenjie, WEI Wenliang, WANG Jinjie, et al. Effect of cobalt particle morphology on the properties of polycrystalline diamond composite [J]. Diamond & Abrasives Engineering,2023,43(4):489-496. doi: 10.13394/j.cnki.jgszz.2022.0216
[5]	徐根, 陈枫, 徐国平, 等. 采用应力释放法测量PDC热残余应力 [J]. 石油钻探技术,2010,38(1):67-71. doi: 10.3969/j.issn.1001-0890.2010.01.017 XU Gen, CHEN Feng, XU Guoping, et al. Researches on measuring residual stresses of polycrystalline diamond compacts using stress-release method [J]. Petroleum Drilling Techniques,2010,38(1):67-71. doi: 10.3969/j.issn.1001-0890.2010.01.017
[6]	徐国平, 尹志民, 陈启武, 等. 金刚石复合片(PDC)表面残余应力的XRD研究 [J]. 粉末冶金技术,2010,28(1):16-20. doi: 10.19591/j.cnki.cn11-1974/tf.2010.01.004 XU Guoping, YIN Zhimin, CHEN Qiwu, et al. Investigation of residual stress distribution on the surface of polycrystalline diamond compact using XRD [J]. Powder Metallurgy Technology,2010,28(1):16-20. doi: 10.19591/j.cnki.cn11-1974/tf.2010.01.004
[7]	PAGGETT J W, DRAKE E F, KRAWITZ A D, et al. Residual stress and stress gradients in polycrystalline diamond compacts [J]. International Journal of Refractory Metals & Hard Materials,2002,20(3):187-194. doi: 10.1016/S0263-4368(01)00077-4
[8]	贾洪声, 鄂元龙, 华中, 等. 金刚石烧结体残余应力的Raman表征 [J]. 超硬材料工程,2012,24(6):6-9. doi: 10.3969/j.issn.1673-1433.2012.06.002 JIA Hongsheng, E Yuanlong, HUA Zhong, et al. Raman characterization of the residual stress of sintered diamonds [J]. Superhard Material Engineering,2012,24(6):6-9. doi: 10.3969/j.issn.1673-1433.2012.06.002
[9]	罗德, 张菁, 黎明发, 等. 聚晶金刚石复合片残余热应力的影响因素 [J]. 煤田地质与勘探,2010,38(5):67-70. doi: 10.3969/j.issn.1001-1986.2010.05.015 LUO De, ZHANG Jing, LI Mingfa, et al. Analysis of the influencing factors of residual thermal stress of polycrystalline diamond compact [J]. Coal Geology & Exploration,2010,38(5):67-70. doi: 10.3969/j.issn.1001-1986.2010.05.015
[10]	江民圣. ANSYS Workbench 19.0基础入门与工程实践[M]. 北京: 人民邮电出版社, 2019. JIANG Minsheng. ANSYS Workbench 19.0 fundamentals and engineering practice [M]. Beijing: Posts & Telecom Press, 2019.
[11]	张菁, 黎明发, 孙振亚, 等. 优化设计在PDC残余热应力计算中的应用 [J]. 武汉理工大学学报(信息与管理工程版),2011,33(5):750-753. doi: 10.3963/j.issn.1007-144X.2011.05.019 ZHANG Jing, LI Mingfa, SUN Zhenya, et al. Application of optimal design in residual thermal stress calculation on polycrystalline diamond compact [J]. Journal of Wuhan University of Technology (Information & Management Engineering),2011,33(5):750-753. doi: 10.3963/j.issn.1007-144X.2011.05.019
[12]	罗德. 聚晶金刚石复合片及其钻头的应用研究[D]. 武汉: 武汉理工大学, 2010. LUO De. Research and application of PDC and PDC Bits [D]. Wuhan: Wuhan University of Technology, 2010.
[13]	徐国平, 陈启武, 尹志民, 等. 金刚石层厚度对复合片(PDC)残余应力的影响 [J]. 高压物理学报,2009,23(2):24-30. doi: 10.3969/j.issn.1000-5773.2009.01.004 XU Guoping, CHEN Qiwu, YIN Zhimin, et al. The effect of thickness of diamond layer on residual stresses in polycrystalline diamond compact [J]. Chinese Journal of High Pressure Physics,2009,23(2):24-30. doi: 10.3969/j.issn.1000-5773.2009.01.004