Study on the influence of grinding disc motion on the forming of silicon nitride ceramic balls
-
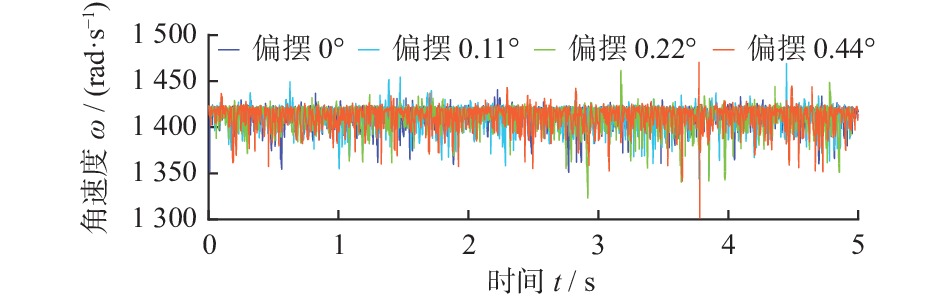
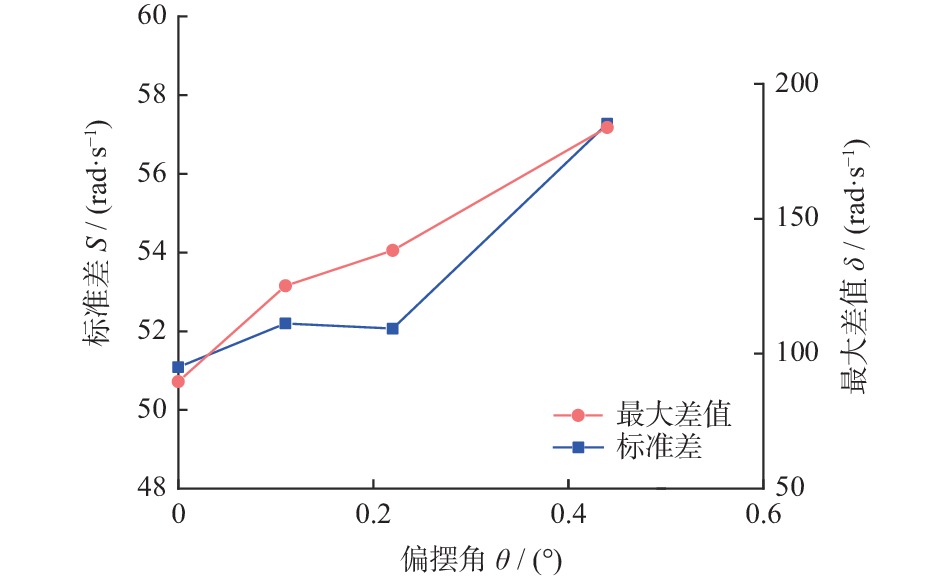
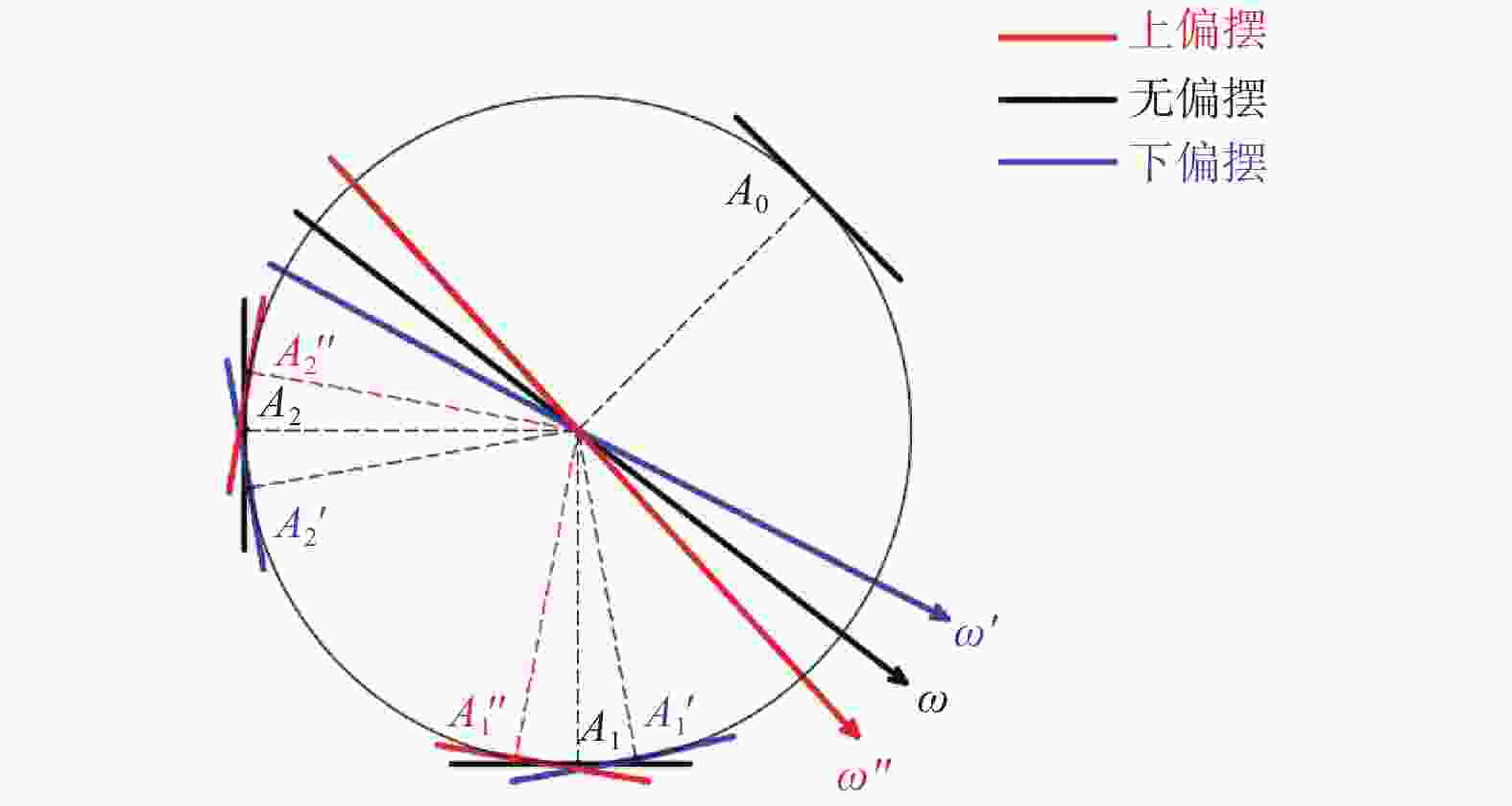
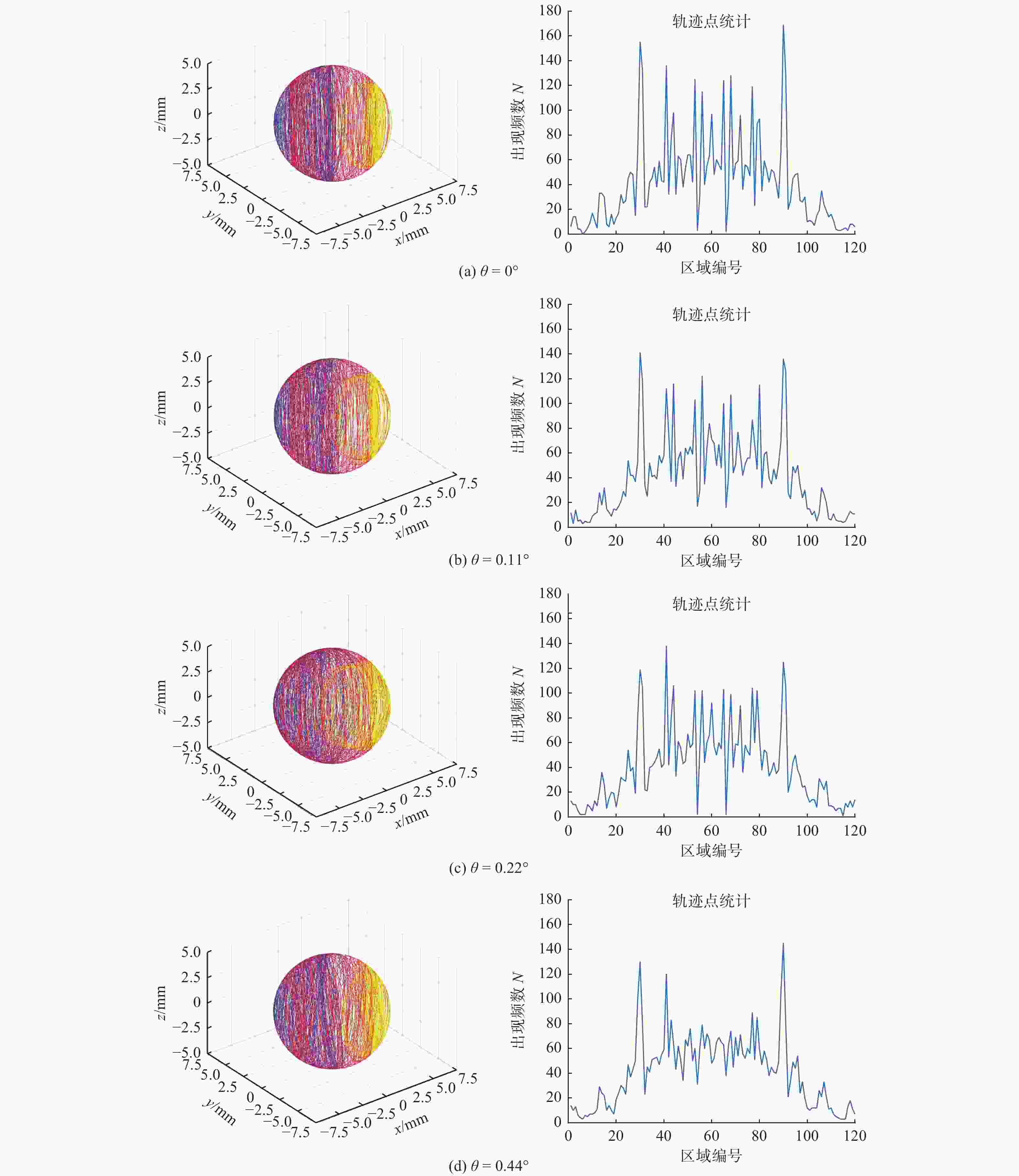
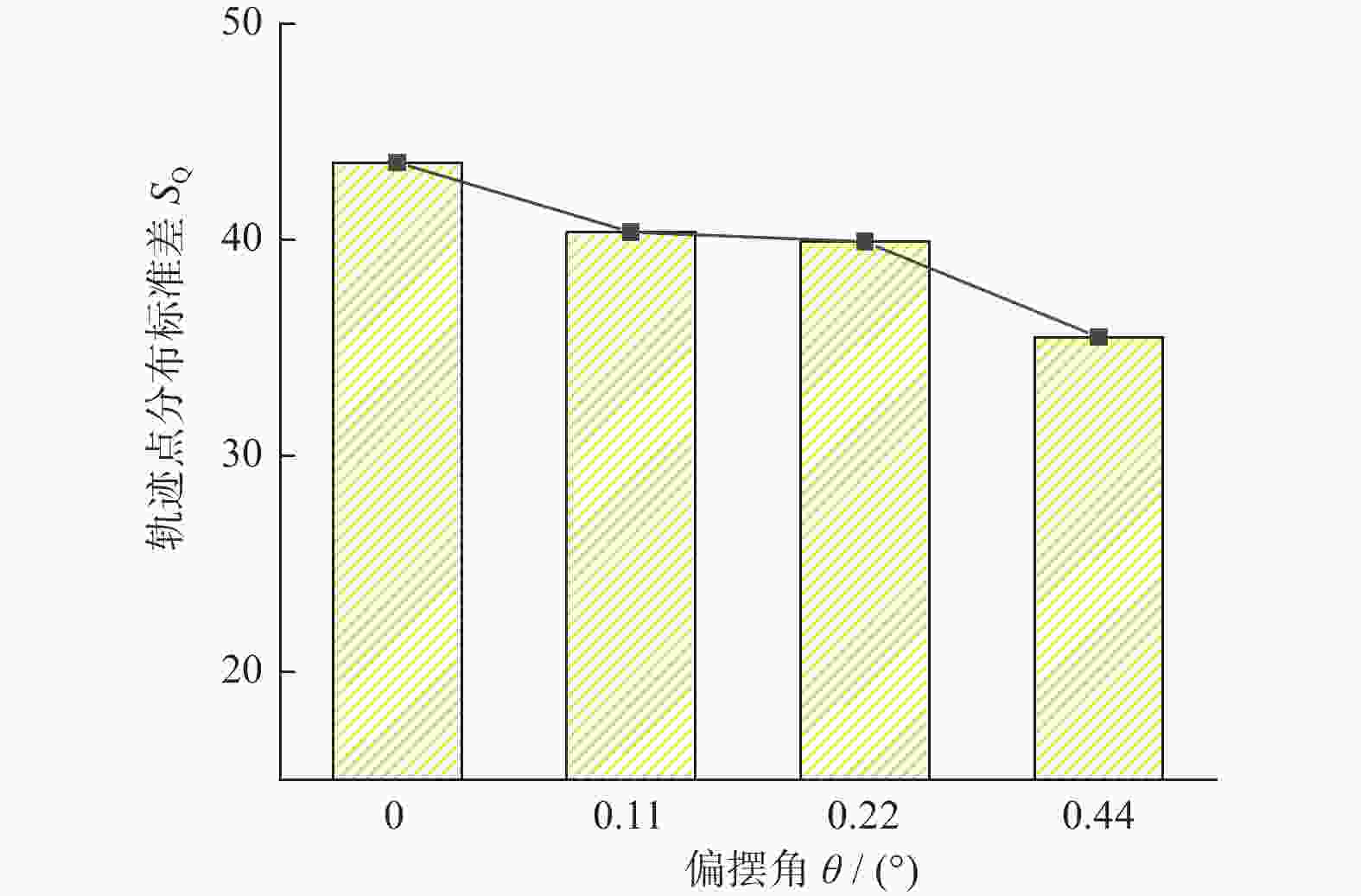
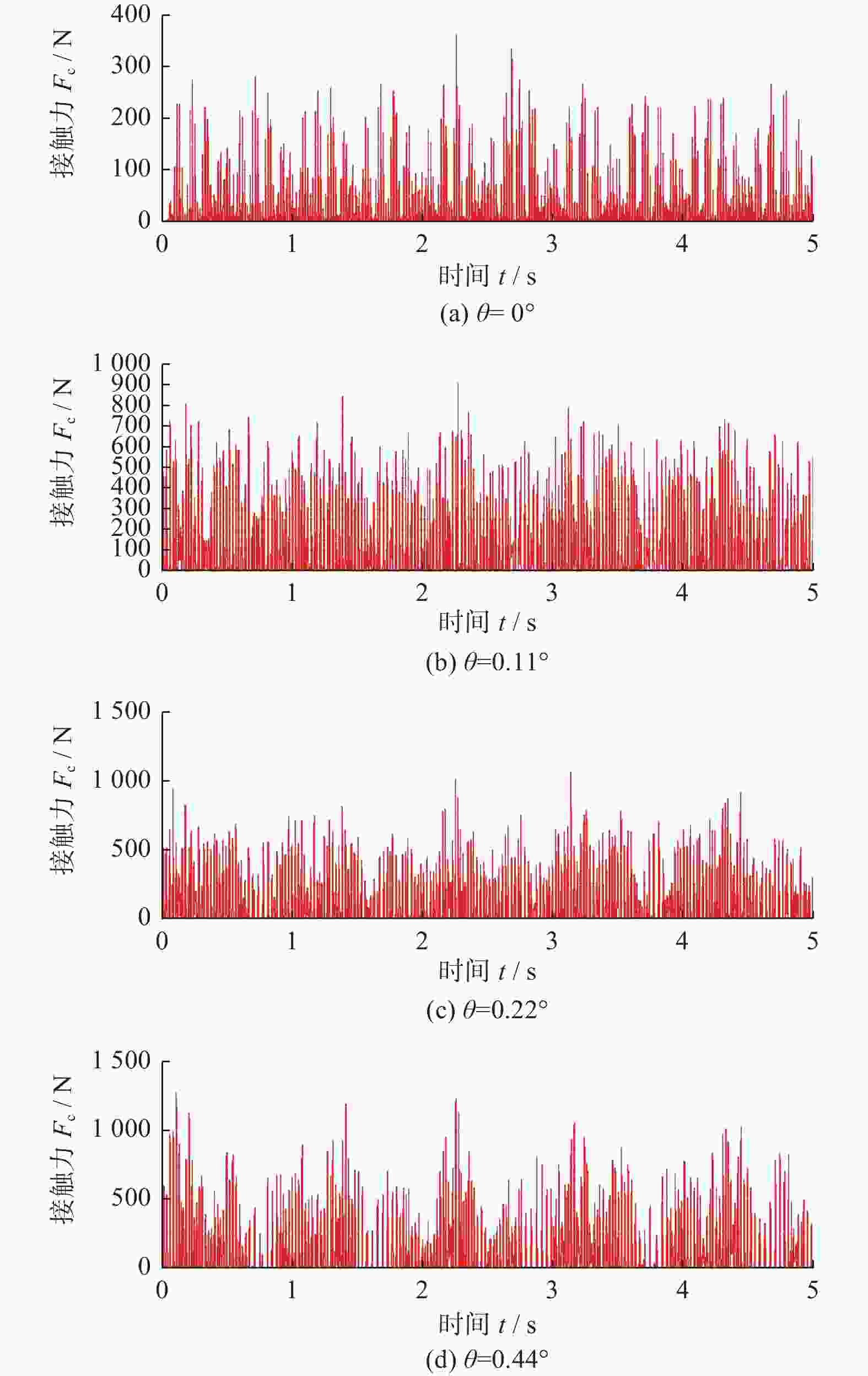
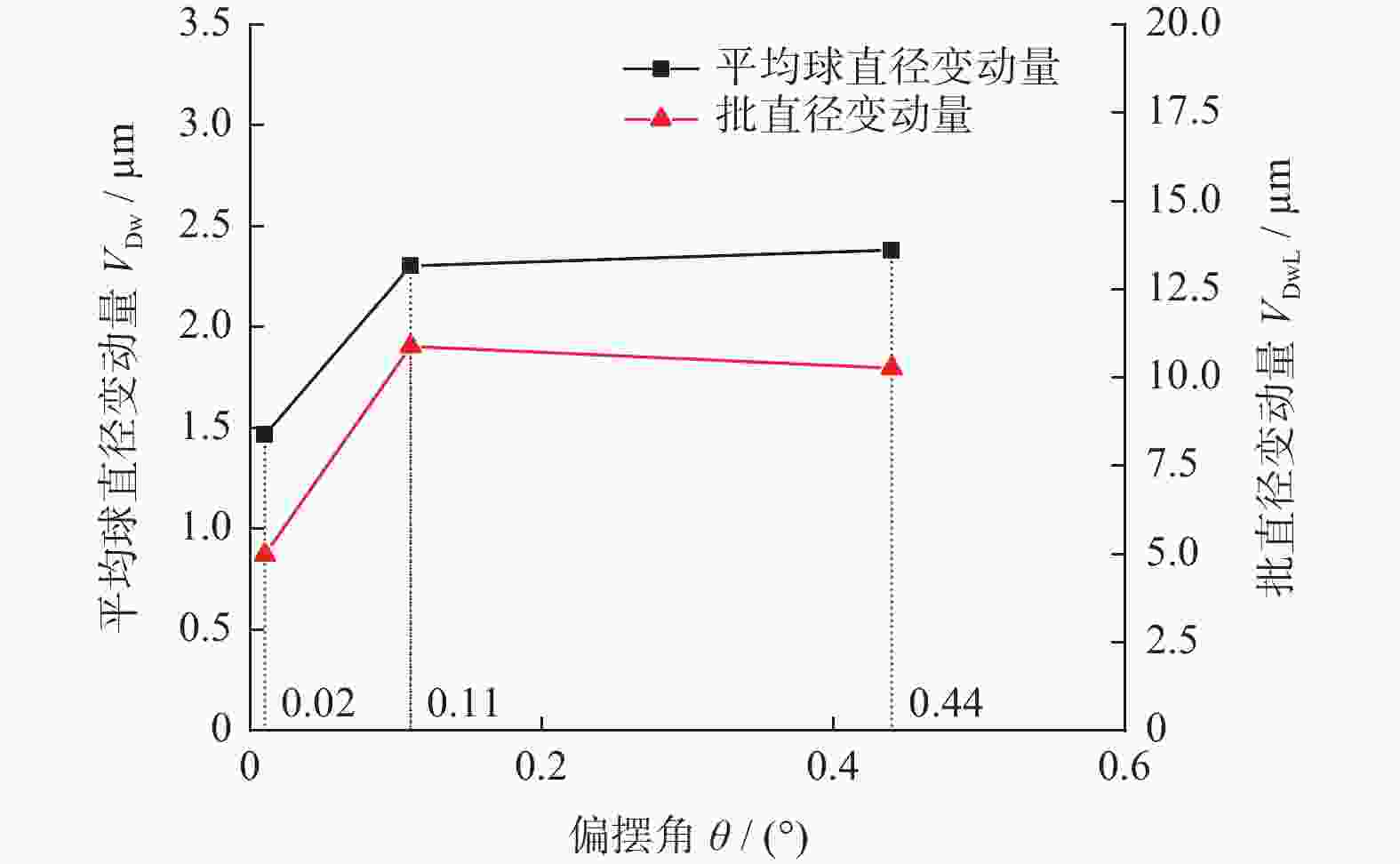
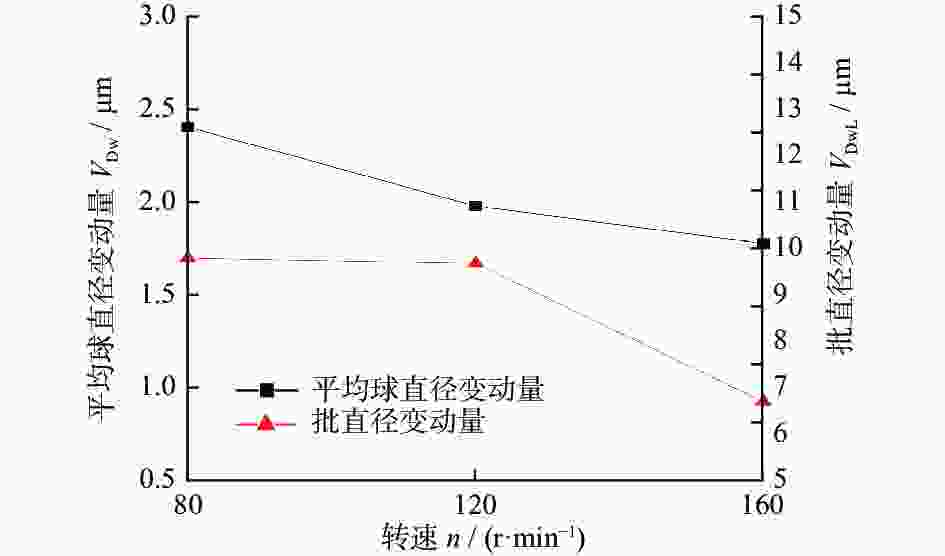
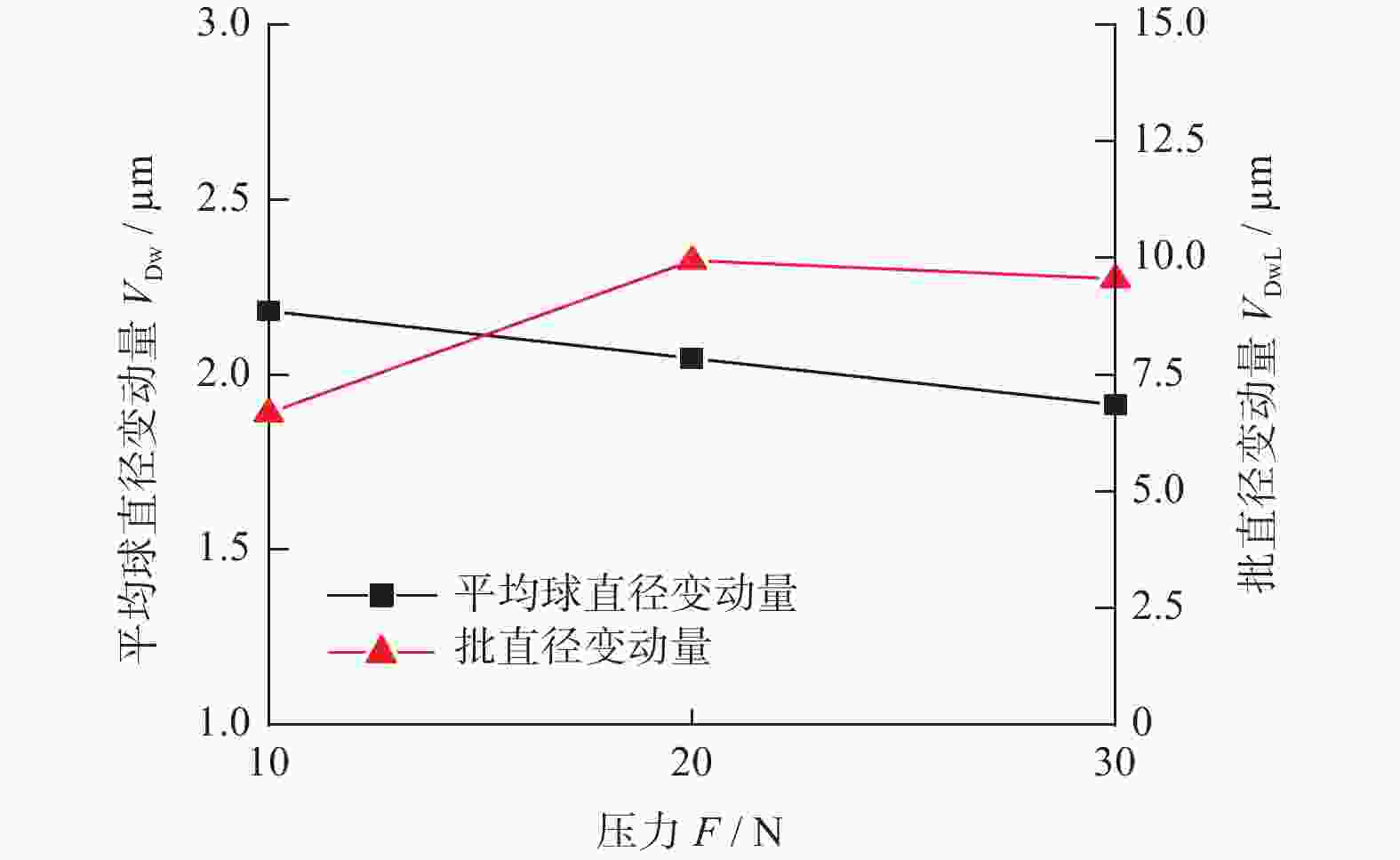
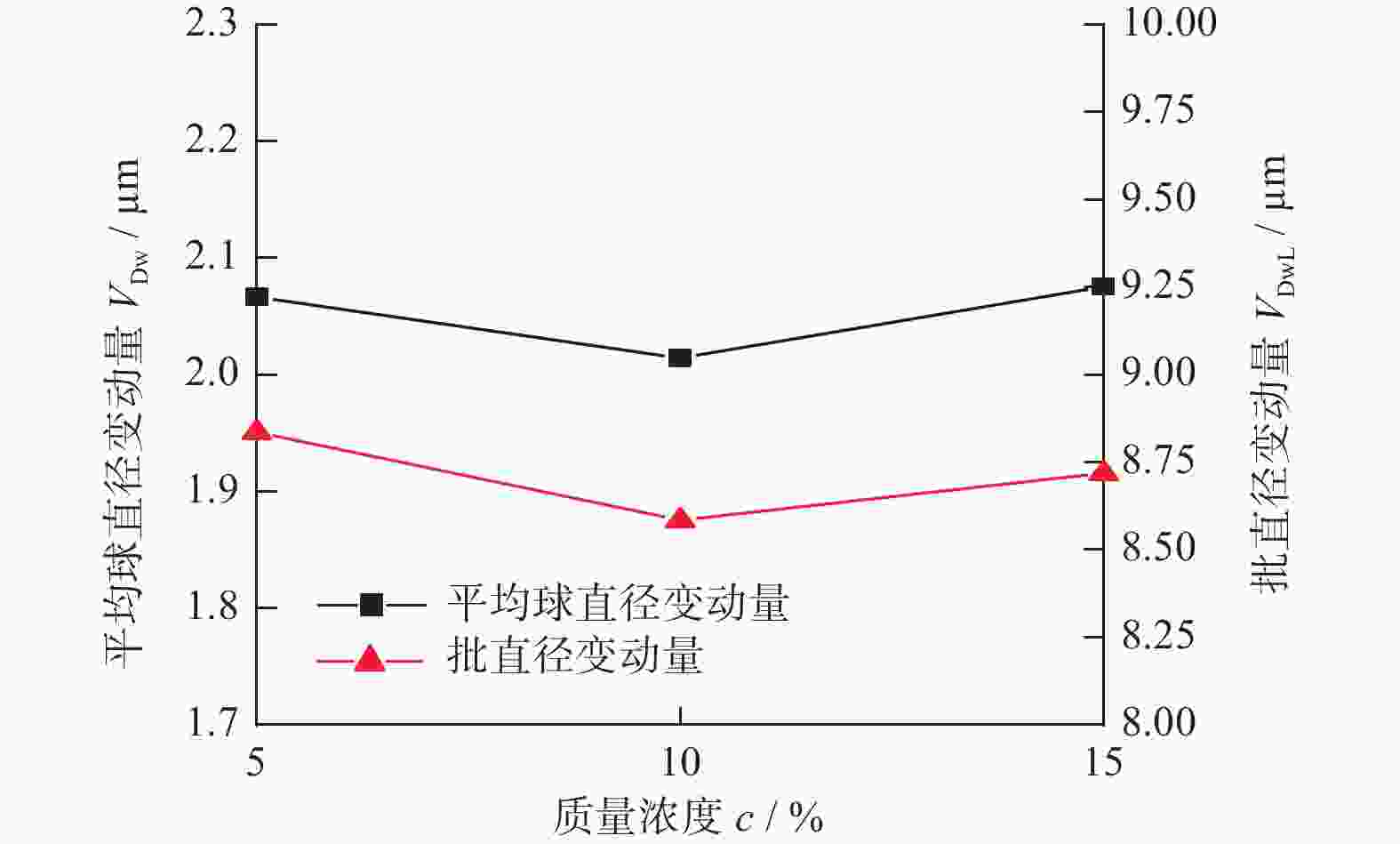
摘要: 为提高氮化硅陶瓷球加工精度,提出研磨盘偏摆运动可控的新型锥形柔性支承研磨方式,探究柔性支承研磨方式下陶瓷球成形机理。基于新型研磨方式建立仿真模型,深入分析研磨盘偏摆运动对于氮化硅陶瓷球研磨轨迹与受力状态影响。在搭建的新型锥形柔性支承研磨平台上进行正交实验,进一步分析研磨盘运动特性对球体成形的影响。仿真与实验结果表明:在柔性支承研磨方式下,随着研磨盘偏摆角增大,球体轨迹均匀性标准差从43.58降至35.49,最大接触力提升至初始值的4倍,陶瓷球平均球直径变动量从1.466 μm增至2.382 μm,批直径变动量从4.98 μm增至10.27 μm。研磨盘偏摆运动有利于优化研磨轨迹,但增大了球体受力的不均匀性,不利于改善氮化硅陶瓷球平均球直径变动量与批直径变动量,在实际加工过程中,研磨盘偏摆角需控制在0.02°以内。Abstract: In order to improve the processing accuracy of silicon nitride ceramic balls and to investigate the mechanism of forming ceramic balls by flexible support grinding method, a new cone-type flexible support grinding method with controlled deflection motion of grinding disc is proposed. Based on the new grinding method, a simulation model is established to deeply analyze the influence of the deflection motion of the grinding disc on the grinding trajectory and force state of the silicon nitride ceramic balls. Orthogonal experiments were conducted on a new cone-type flexible support grinding platform built to further analyze the effect of grinding disc motion characteristics on ball formation. Simulation and experimental results show that under the flexible support grinding method, As the increases of grinding disc deflection angle, the standard deviation of ball trajectory uniformity decreased from 43.58 to 35.49, the maximum contact force increased to 4 times the initial value, the average ball diameter variation increased from 1.466 μm to 2.382 μm, and the batch diameter variation increased from 4.98 μm to 10.27 μm. The lower grinding disc deflection motion is beneficial to optimize the grinding trajectory, but increases the unevenness of the ball force, which is not conducive to improving the average ball diameter variation and batch diameter variation of silicon nitride ceramic balls. In the actual process, the angle of deflection of the grinding disc must be controlled to within 0.02°.
-
表 1 氮化硅陶瓷球物理性能
Table 1. Physical properties of silicon nitride ceramic ball
参数 参数值 密度 ρ / (g∙cm−3) 3.26 弹性模量 E / GPa 310 硬度 H / GPa 16 泊松比 ε 0.25 断裂韧性 KIC / (MPa∙m−2) 7.0 热膨胀系数 λ / K−1 3.2 × 10−6 表 2 正交实验因素水平表
Table 2. Table of orthogonal experimental factor levels
水平 因素 下盘偏摆角
θ / (°)
A研磨盘转速
n / (r·min−1)
B压力
F / N
C质量浓度
c / %
D1 0.02 80 10 5 2 0.11 120 20 10 3 0.44 160 30 15 表 3 平均球直径变动量正交回应表
Table 3. Orthogonal response table for mean average ball diameter variation
水平 因素 下盘偏
摆角A转速
B压力
C研磨液质量
浓度D1 1.466 2.402 2.181 2.065 2 2.304 1.976 2.049 2.013 3 2.382 1.774 1.921 2.074 极差 0.916 0.628 0.260 0.061 表 4 批直径变动量正交回应表
Table 4. Orthogonal response table for batch diameter variation
水平 因素 下盘偏
摆角A转速
B压力
C研磨液
浓度D1 4.98 9.78 6.73 8.83 2 10.88 9.67 9.90 8.58 3 10.27 6.68 9.53 8.72 极差 5.90 3.10 3.17 0.25 -
[1] 孙健, 陈伟, 姚金梅, 等. Si3N4陶瓷球研磨轨迹分析及其对表面质量影响机制研究 [J]. 表面技术, 2023, 52(1): 253-265.SUN Jian, CHEN Wei, YAO Jinmei, et al. Analysis of grinding trajectories of Si3N4 ceramic balls and study of its influence mechanism on surface quality [J]. Surface Technology, 2023, 52(1): 253-265. [2] HU F, XIE Z P, ZHANG J, et al. Promising high-thermal-conductivity substrate material for high-power electronic device: silicon nitride ceramics [J]. Rare Metals,2020,39(5):11-26. [3] 张珂, 王定文, 李颂华, 等. 氮化硅陶瓷球研磨去除方式 [J]. 金刚石与磨料磨具工程,2019,39(3):38-44.ZHANG Ke, WANG Dingwen, LI Songhua, et al. Grinding removal method of silicon nitride ceramic balls [J]. Diamond & Abrasives Engineering,2019,39(3):38-44. [4] 李声超, 邓朝晖, 万林林, 等. 氮化硅陶瓷球面磨削表面破碎损伤研究 [J]. 金刚石与磨料磨具工程,2013,33(1):70-74.LI Shengchao, DENG Zhaohui, WAN Linlin, et al. Study on surface fragmentation damage of silicon nitride ceramic spherical grinding [J]. Diamond & Abrasives Engineering,2013,33(1):70-74. [5] LEVESQUE G, ARAKERE N K. An investigation of partial cone cracks in silicon nitride balls [J]. International Journal of Solids and Structures,2008,45(25):6301-6315. [6] KANG J, HADFIELD M. The effects of lapping load in finishing advanced ceramic balls on a novel eccentric lapping machine [J]. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture,2005,219(7):505-513. doi: 10.1243/095440505X32427 [7] WU Y H, LI S H, ZHANG K. Lapping machining of high-speed and high-precision ceramic bearing balls [J]. Key Engineering Materials, 2005, 291-292: 325-330. [8] LV B H, YUAN J L, CHENG F, et al. Influence of supporting characteristics on sphericity of ceramic balls in rotated dual-plates lapping process [J]. Advanced Materials Research, 2009, 69/70: 69-73. [9] ZHOU F, YAO W, YUAN J, et al. Establishment of material removal model for lapping ceramic balls with variable-radius groove plate [J]. The International Journal of Advanced Manufacturing Technology,2020,111:2577-2587. doi: 10.1007/s00170-020-06259-w [10] ZHOU F, YUAN J, LYU B H, et al. Kinematics and trajectory in processing precision balls with eccentric plate and variable-radius V-groove [J]. The International Journal of Advanced Manufacturing Technology,2016,84(9):2167-2178. [11] UMEHARA N, KIRTANE T, GERLICK R, et al. A new apparatus for finishing large size/large batch silicon nitride (Si3N4) balls for hybrid bearing applications by magnetic float polishing (MFP) [J]. International Journal of Machine Tools & Manufacture,2006,46(2):151-169. [12] CHILDS T, MOSS D J. Grinding ratio and cost issues in magnetic and non-magnetic fluid grinding [J]. CIRP Annals - Manufacturing Technology,2000,49(1):261-264. doi: 10.1016/S0007-8506(07)62942-4 [13] BO Z, NAKAJIMA A. Dynamics of magnetic fluid support grinding of Si3N4 ceramic balls for ultraprecision bearings and its importance in spherical surface generation [J]. Precision Engineering,2003,27(1):1-8. doi: 10.1016/S0141-6359(02)00152-6 [14] 马红毅, 麻辉. 实现加工中心机床俯仰、偏摆、倾斜的自动测量 [J]. 制造技术与机床,2009(9):31-35.MA Hongyi, MA Hui. Automatic measurement of pitch, deflection and tilt of machining centre machines [J]. Manufacturing Technology and Machine Tools,2009(9):31-35. [15] 汤科锋. 双自转研磨方式下研磨成球机理的研究 [D]. 杭州: 浙江工业大学, 2010.TANG Kefeng. Study on the mechanism of pellet formation under double rotation grinding [D]. Hangzhou: Zhejiang University of Technology, 2010 [16] 吴天凤, 李莉, 杨洪涛. 数控机床XY工作台单向运动二维阿贝误差分析与建模 [J]. 光学精密工程,2021,29(2):329-337. doi: 10.37188/OPE.20212902.0329WU Tianfeng, LI Li, YANG Hongtao. Analysis and modeling of two-dimensional Abbe error in unidirectional motion of XY table of CNC machine tools [J]. Optical Precision Engineering,2021,29(2):329-337. doi: 10.37188/OPE.20212902.0329 [17] 张珂, 徐湘辉, 吴玉厚, 等. 精密陶瓷球的锥形研磨技术研究 [J]. 金刚石与磨料磨具工程,2005(2):39-42. doi: 10.3969/j.issn.1006-852X.2005.02.012ZHANG Ke, XU Xianghui, WU Yuhou, et al. Research on conical grinding technology of precision ceramic balls [J]. Diamond & Abrasives Engineering,2005(2):39-42. doi: 10.3969/j.issn.1006-852X.2005.02.012 [18] 常敏, 吕冰海, 王志伟, 等. 陶瓷球研磨成型机理的研究 [J]. 机械工程师,2003(9):47-50.CHANG Min, LYU Binghai, WANG Zhiwei, et al. Study on the mechanism of ceramic ball grinding and forming [J]. Mechanical Engineer,2003(9):47-50. [19] 聂兰芳, 赵学军. 钢球加工成圆条件及其影响因素探讨 [J]. 轴承,2001(1):16-18.NIE Lanfang, ZHAO Xuejun. The rounding conditions of steel balls and their influencing factors [J]. Bearings,2001(1):16-18. [20] 朱晨. 钢球研磨力学原理 [M]. 郑州: 河南科学技术出版社, 1995.ZHU Chen. Principles of steel ball grinding mechanics [M]. Zhengzhou: Henan Science and Technology Press, 1995. [21] 吴玉厚, 沙勇, 李颂华, 等. 氮化硅陶瓷球研磨过程中微磨料磨损形式的转变 [J]. 兵器材料科学与工程,2021,44(3):49-57. doi: 10.14024/j.cnki.1004-244x.20210312.001WU Yuhou, SHA Yong, LI Songhua, et al. Transformation of micro-abrasive wear forms in silicon nitride ceramic ball grinding process [J]. Weapons Materials Science and Engineering,2021,44(3):49-57. doi: 10.14024/j.cnki.1004-244x.20210312.001 -



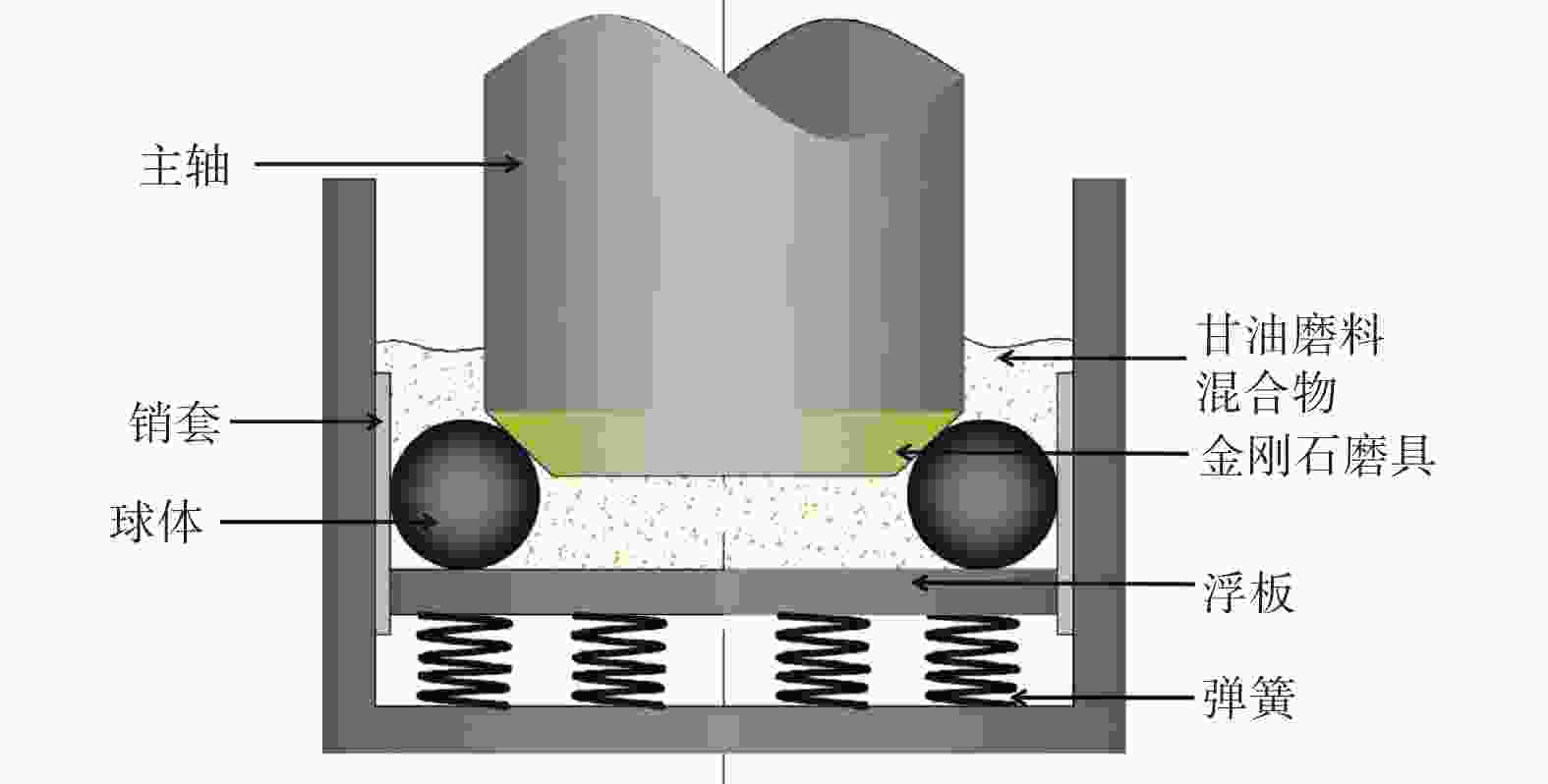
 下载:
下载:
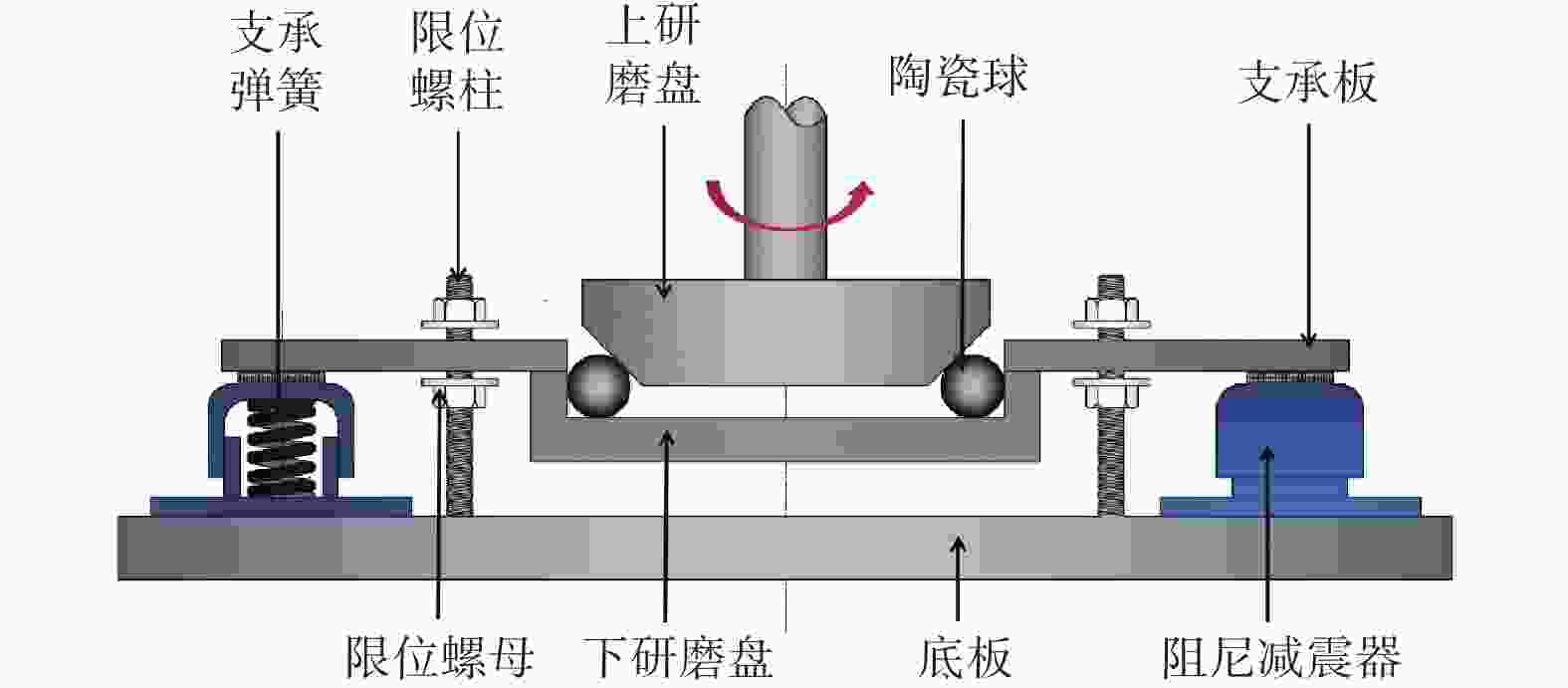
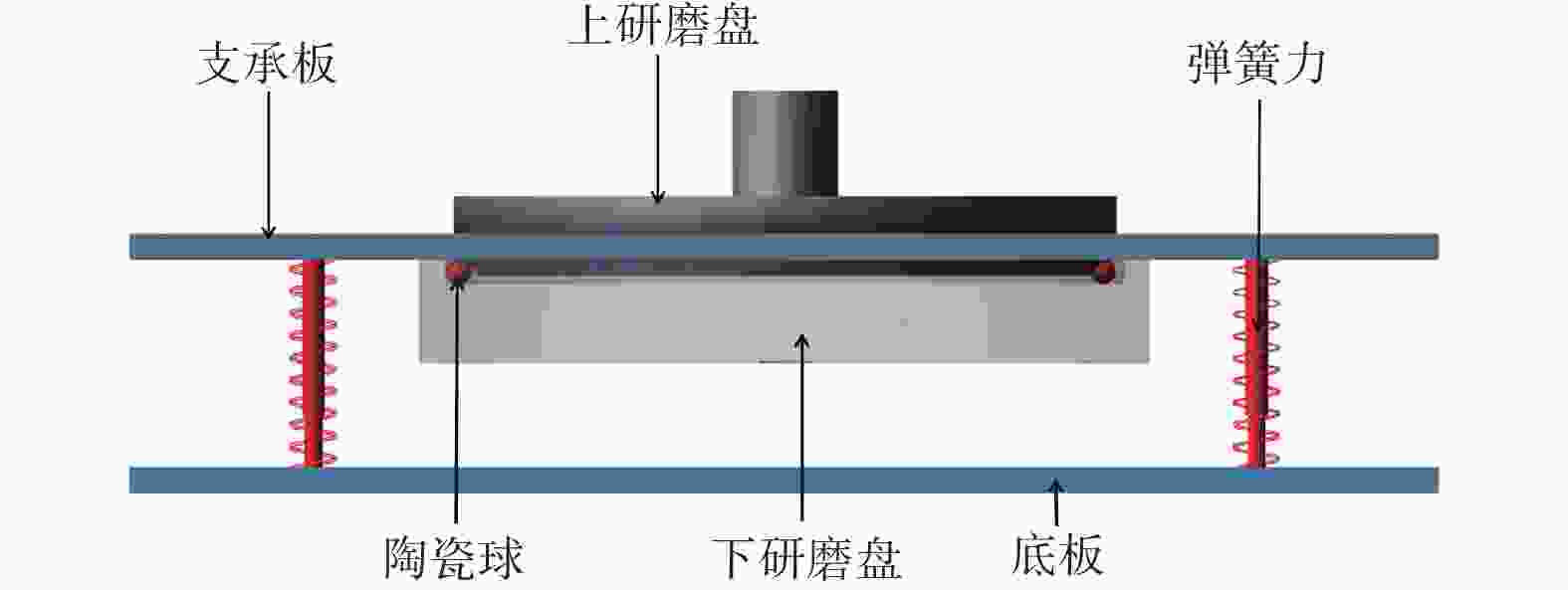
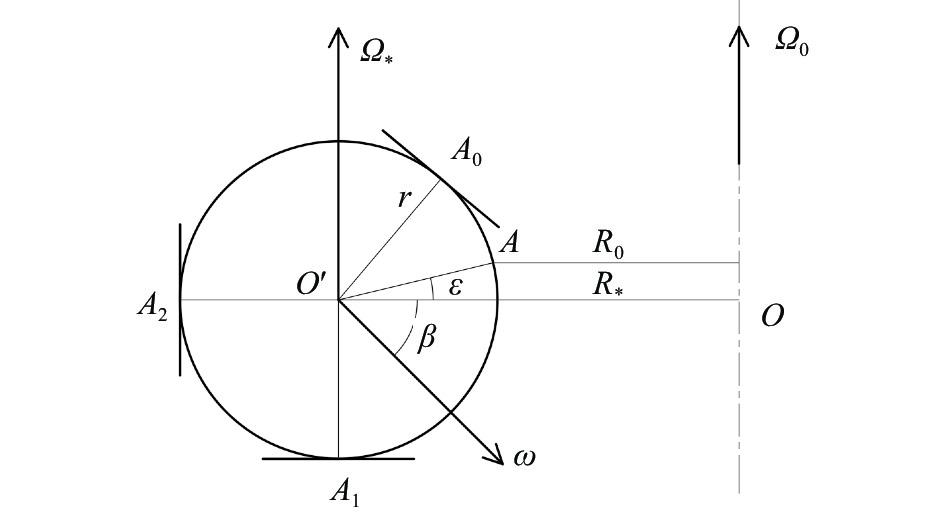





 邮件订阅
邮件订阅 RSS
RSS
