Optimization of hinge beam of cylinder-beam integrated cubic press based on response surface method
-
摘要:
六面顶压机是中国生产金刚石的主要设备,其关重件铰链梁在工作中承受连续的交变载荷,易出现失效破损。提出RSM和MOGA相结合的方法,对新型六面顶压机的铰链梁进行优化分析。首先建立铰链梁的参数化模型,以关键部分的尺寸为设计参数,以最大应力和最大位移为目标函数,并对其最大质量进行约束;然后使用DOE获得设计试验点;利用RSM获得代理模型;再通过MOGA法搜索全局最优解,最后对铰链梁的优化结果进行评估。结果表明:优化后的铰链梁在质量略微增加的情况下,刚度和强度有效提高,应力集中现象也明显改善。
Abstract:Cubic press is the primary equipment for diamond production in China. Its key component, the hinge beam, bears continuous alternating loads in the working environment and is prone to failure and breakage. In this paper, a method combining response surface method (RSM) and multi-objective genetic algorithms (MOGA) is proposed to optimize the hinge beam of the new hexagon top press. Firstly, the parametric model of the hinge beam is established, with the dimensions of key parts as design parameters, the maximum stress and displacement as objective functions, and the maximum mass is constrained. Then, the optimal space-filling design (OSF) is used as the design of experiments (DOE) to obtain the design experimental points. The proxy model is obtained by the response surface method. Afterward, the global optimum solution is searched using the MOGA method, and the optimal result of the hinge beam is evaluated. The results show that the stiffness and strength of the optimized hinge beam are effectively improved with a slight increase in weight, and the stress concentration is also significantly reduced, providing a useful reference for the design and development of the press.
-
Key words:
- cubic press /
- hinge beam /
- response surface method /
- multi-objective genetic algorithms
-
表 1 材料参数表
Table 1. Material parameters
材料 密度
ρ / (kg·m−3)弹性模量
E / MPa泊松比
$ \upsilon $屈服强度
$ \sigma $s / MPa42CrMo 7.85 × 103 2.1 × 105 0.3 724 40Cr 7.85 × 103 2.1 × 105 0.3 785 表 2 设计参数上限与下限
Table 2. Upper and lower limits of design parameters
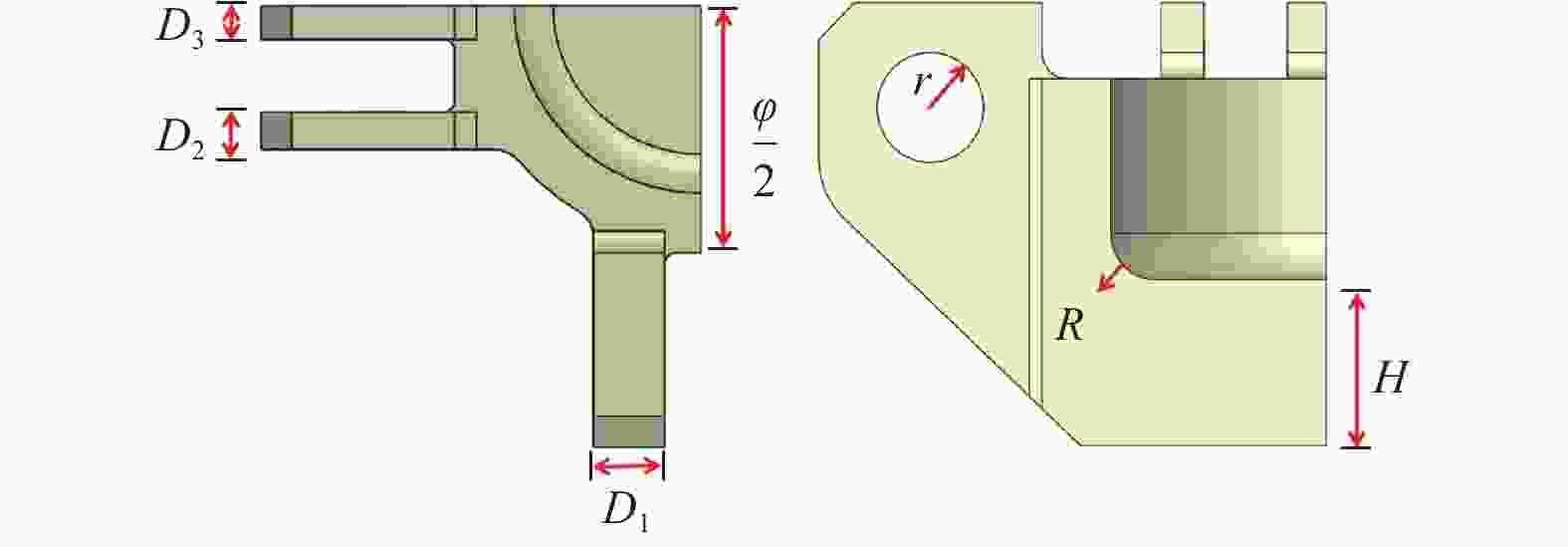
参数 上限值 初始值 下限值 凸耳的厚度 D1 / mm 176.00 160.00 144.00 凸耳的厚度 D2 / mm 99.00 90.00 81.00 凸耳的厚度 D3 / mm 88.00 80.00 72.00 销孔半径 r / mm 107.25 97.50 87.75 底部圆角半径 R / mm 93.50 85.00 76.50 缸体的外径 φ / mm 1 287.00 1 170.00 1 053.00 缸底厚度 H / mm 300.00 255.00 235.00 表 3 Pareto最优解
Table 3. Pareto optimal solution
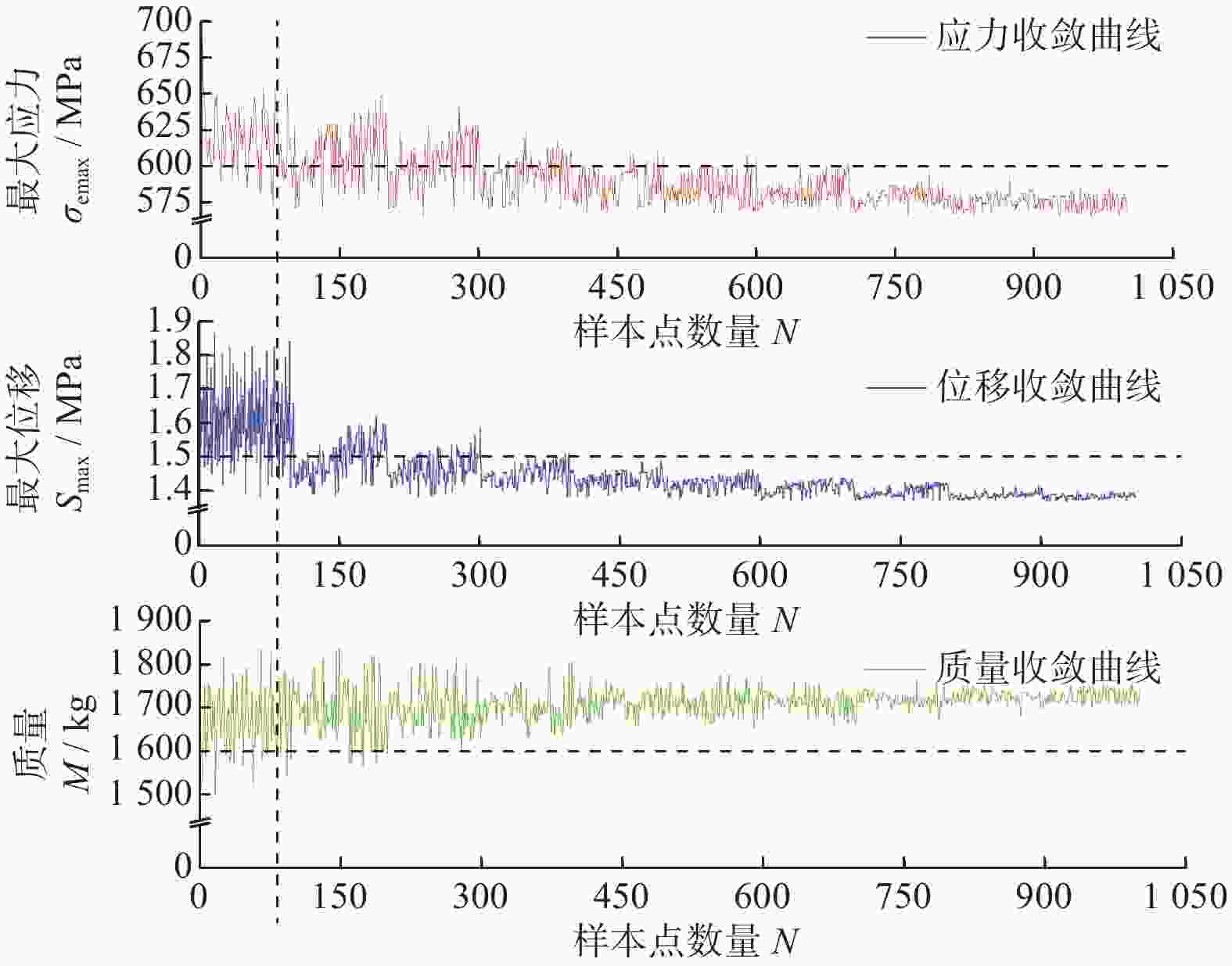
优化目标 候选点1 候选点2 候选点3 最大应力 $ {\sigma }_{\mathrm{emax}} $ / MPa 576.87 570.29 571.71 最大位移 $ {S}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ / mm 1.37 1.37 1.38 质量 M / kg 1 719.60 1 739.20 1 726.40 表 4 优化结果
Table 4. Optimization results
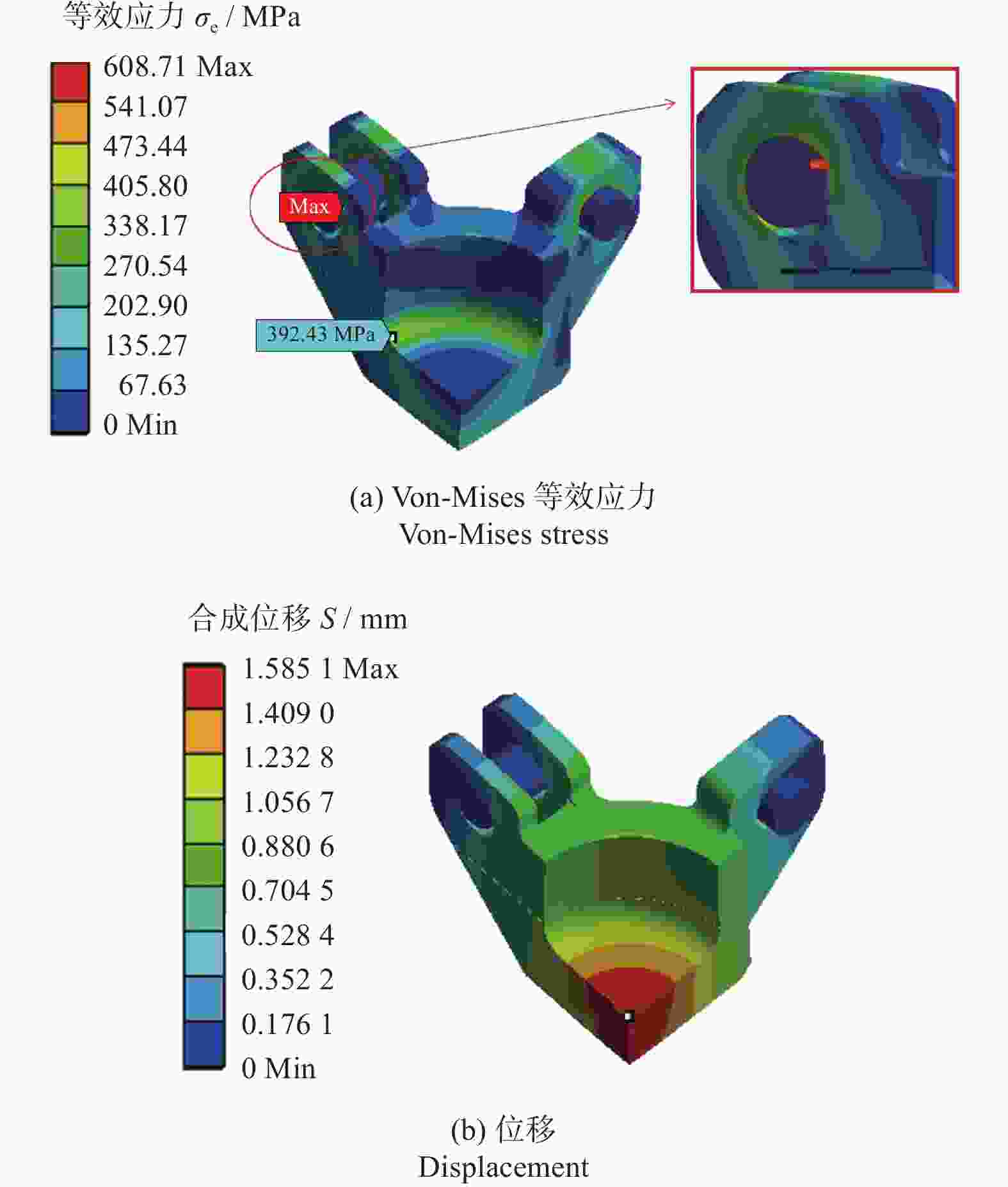
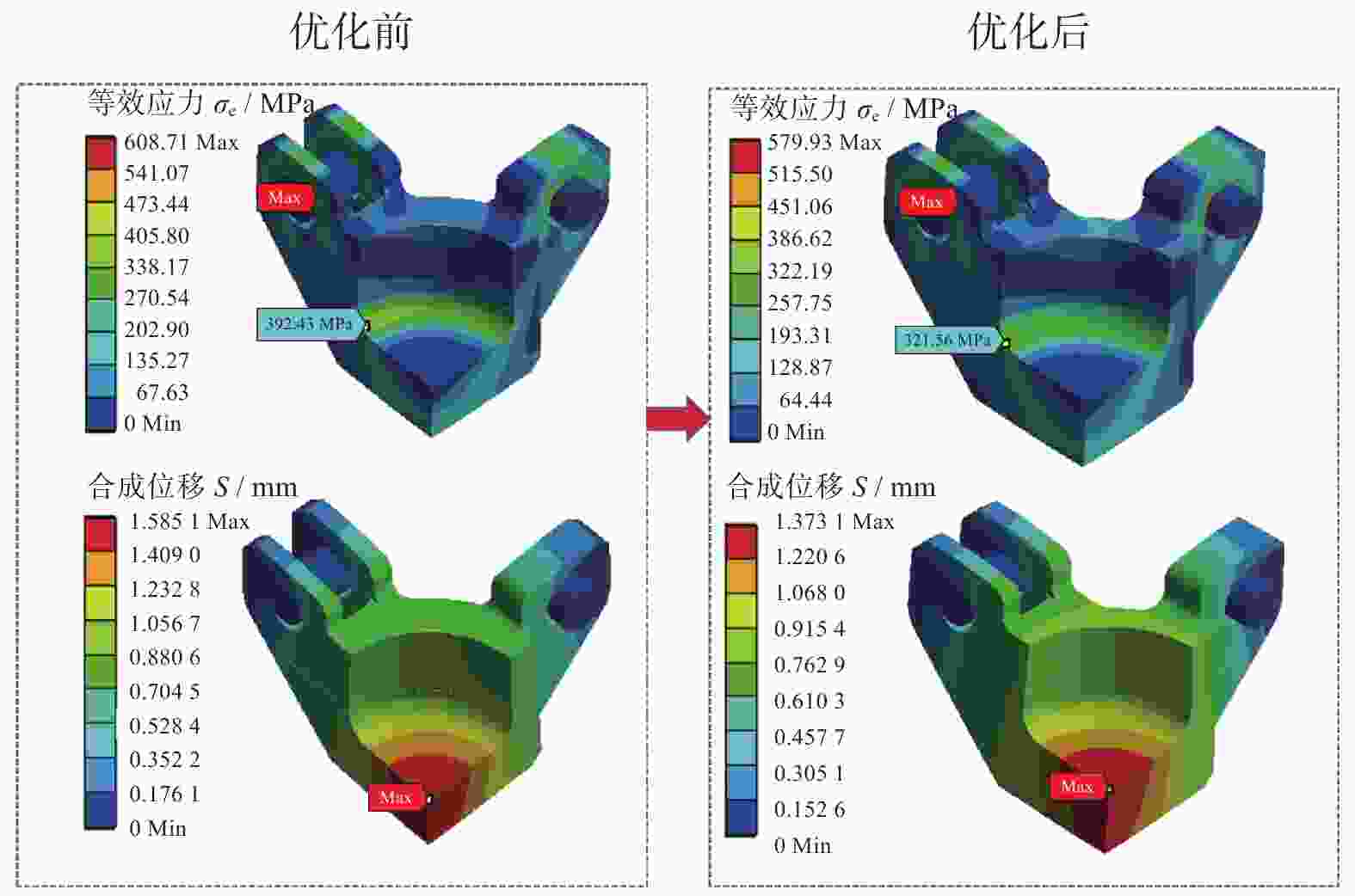
名称 优化前 优化后 圆整后 凸耳的厚度 D1 / mm 160.00 171.83 172.00 凸耳的厚度 D2 / mm 90.00 97.43 97.50 凸耳的厚度 D3 / mm 80.00 87.27 87.50 底部圆角半径 R / mm 85.00 92.43 92.50 销孔半径 r / mm 97.50 88.55 88.50 缸体的外径 φ / mm 1 170.00 1 071.00 1 071.00 缸底厚度 H / mm 255.00 295.23 295.00 最大应力 ${\sigma }_{\mathrm{emax} }$ / MPa 608.71 576.87 579.93 最大位移 $ {S}_{\mathrm{m}\mathrm{a}\mathrm{x}} $/ mm 1.59 1.37 1.37 质量 M / kg 1 670.30 1 719.60 1 721.00 -
[1] 方啸虎, 温简杰. 我国六面顶压机大型化的优势及压机继续大型化的难点和对策 [J]. 超硬材料工程,2012,24(1):31-35. doi: 10.3969/j.issn.1673-1433.2012.01.008FANG Xiaohu, WEN Jianjie. The advantages of the large-scale cubic press in China and the difficulties and countermeasures for the continued large-scale press [J]. Superhard Material Engineering,2012,24(1):31-35. doi: 10.3969/j.issn.1673-1433.2012.01.008 [2] WANG Y, KOU Z, ZHANG J, et al. A new pressurization-insulation and pre-sealing system to improve pressure in cubic press from 6 GPa to 12 GPa [J]. Review of Scientific Instruments,2020,91(3):035119. doi: 10.1063/5.0001958 [3] 王良文, 刘建设, 汪曙光, 等. UDS-Ⅲ型金刚石压机结构的有限元分析 [J]. 机械设计,2005(3):38-41. doi: 10.3969/j.issn.1001-2354.2005.03.014WANG Liangwen, LIU Jianshe, WANG Shuguang, et al. Finite element analysis of the structure of UDS-Ⅲ diamond press [J]. Journal of Machine Design,2005(3):38-41. doi: 10.3969/j.issn.1001-2354.2005.03.014 [4] 刘竹丽, 梁颖, 秦东晨. 基于有限元法的铰链梁疲劳强度分析与设计研 [J]. 金刚石与磨料磨具工程,2006(4):38-42. doi: 10.13394/j.cnki.jgszz.2006.04.012LIU Zhuli, LIANG Ying, QIN Dongchen. Fatigue strength analysis and design research of hinge beam based on finite element method [J]. Diamond & Abrasives Engineering,2006(4):38-42. doi: 10.13394/j.cnki.jgszz.2006.04.012 [5] 张聪, 马红安, 韩奇钢, 等. 高压下国产六面顶压机铰链梁和工作缸的应力分析 [J]. 高压物理学报,2010,24(5):321-325.ZHANG Cong, MA Hongan, HAN Qigang, et al. Stress analysis of the hinge beam and working cylinder of a domestic cubic press under high pressure [J]. Chinese Journal of High Pressure Physics,2010,24(5):321-325. [6] 汪曙光. 基于Ansys Workbench六面顶压机优化分析 [J]. 金刚石与磨料磨具工程,2015,35(2):69-73.WANG Shuguang. Optimization analysis of cubic press based on Ansys Workbench [J]. Diamond & Abrasives Engineering,2015,35(2):69-73. [7] 于浩, 赵军, 盖少磊, 等. 42CrMo钢精车加工表面残余应力有限元仿真研究 [J]. 现代制造工程,2021(11):87-92. doi: 10.16731/j.cnki.1671-3133.2021.11.013YU Hao, ZHAO Jun, GAI Shaoli, et al. Finite element simulation study on residual stress of 42CrMo steel finish turning surface [J]. Modern Manufacturing Engineering,2021(11):87-92. doi: 10.16731/j.cnki.1671-3133.2021.11.013 [8] 董雪娇, 杨大巍, 刘锦燕, 等. 40Cr钢螺栓断裂失效原因分析 [J]. 钢铁钒钛,2020,41(3):172-176.DONG Xuejiao, YANG Dawei, LIU Jinyan, et al. Failure cause analysis of 40Cr steel bolt fracture [J]. Iron Steel Vanadium Titanium,2020,41(3):172-176. [9] 万云发, 孙文磊, 王宏伟, 等. 基于Kriging模型与MOGA算法的风力机主轴轻量化设计 [J]. 太阳能学报,2022,43(3):388-395.WAN Yunfa, SUN Wenlei, WANG Hongwei, et al. Lightweight design of wind turbine spindle based on kriging model and MOGA algorithm [J]. Acta Energiae Solaris Sinica,2022,43(3):388-395. [10] 朱子青, 贺磊, 杨先海, 等. 基于响应面法的伸缩臂架构有限元分析与优化 [J]. 山东理工大学学报(自然科学版),2022,36(1):70-75, 81. doi: 10.13367/j.cnki.sdgc.2022.01.012ZHU Ziqing, HE Lei, YANG Xianhai, et al. Finite element analysis and optimization of telescopic arm structure based on response surface method [J]. Journal of Shandong University of Technology(Natural Science Edition),2022,36(1):70-75, 81. doi: 10.13367/j.cnki.sdgc.2022.01.012 [11] 罗丹. 某复合盾构刀盘有限元分析及参数优化 [J]. 现代隧道技术,2020,57(6):115-119. doi: 10.13807/j.cnki.mtt.2020.06.015LUO Dan. Finite element analysis and parameter optimization of a composite shield cutter head [J]. Modern Tunnelling Technology,2020,57(6):115-119. doi: 10.13807/j.cnki.mtt.2020.06.015 -



 下载:
下载:


 邮件订阅
邮件订阅 RSS
RSS
